I need an analytical estimation of the following integral:
$$\int\limits_0^\infty \frac{{\mathrm{d} x}}{\sqrt{1 + x^4}}$$
It has a root in the denomenator -- so I can't make use of complex residues technique.
Edit:
Since CAS can do it symbolically -- there's certainly a solution. However I did this analytically a couple of years ago and obtained
$$ \frac{\pi}{2^{3/4}}$$
estimation. I remember it was easy and fast estimation. I'm trying to recover it.
$\newcommand{\+}{^{\dagger}}% \newcommand{\angles}[1]{\left\langle #1 \right\rangle}% \newcommand{\braces}[1]{\left\lbrace #1 \right\rbrace}% \newcommand{\bracks}[1]{\left\lbrack #1 \right\rbrack}% \newcommand{\ceil}[1]{\,\left\lceil #1 \right\rceil\,}% \newcommand{\dd}{{\rm d}}% \newcommand{\down}{\downarrow}% \newcommand{\ds}[1]{\displaystyle{#1}}% \newcommand{\equalby}[1]{{#1 \atop {= \atop \vphantom{\huge A}}}}% \newcommand{\expo}[1]{\,{\rm e}^{#1}\,}% \newcommand{\fermi}{\,{\rm f}}% \newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,}% \newcommand{\half}{{1 \over 2}}% \newcommand{\ic}{{\rm i}}% \newcommand{\iff}{\Longleftrightarrow} \newcommand{\imp}{\Longrightarrow}% \newcommand{\isdiv}{\,\left.\right\vert\,}% \newcommand{\ket}[1]{\left\vert #1\right\rangle}% \newcommand{\ol}[1]{\overline{#1}}% \newcommand{\pars}[1]{\left( #1 \right)}% \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}}% \newcommand{\root}[2][]{\,\sqrt[#1]{\,#2\,}\,}% \newcommand{\sech}{\,{\rm sech}}% \newcommand{\sgn}{\,{\rm sgn}}% \newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}} \newcommand{\ul}[1]{\underline{#1}}% \newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$ \begin{align} \int_{0}^{\infty}{\dd x \over \root{1 + x^{4}}}&= {1 \over 4}\int_{0}^{\infty}x^{-3/4}\pars{1 + x}^{-1/2}\,\dd x = {1 \over 4}\int_{1}^{\infty}\pars{x - 1}^{-3/4}x^{-1/2}\,\dd x \\[3mm]&= {1 \over 4}\int_{1}^{0}\pars{{1 \over x} - 1}^{-3/4}x^{1/2}\, \pars{-\,{\dd x \over x^{2}}} = {1 \over 4}\int^{1}_{0}\pars{1 - x}^{-3/4}x^{-3/4}\,\dd x \\[3mm]&= {1 \over 4}\,{\rm B}\pars{{1 \over 4},{1 \over 4}} \quad\mbox{where}\quad{\rm B}\pars{a,b}\quad\mbox{is the}\ {\it Beta\ function}. \end{align} Also $$ {\rm B}\pars{{1 \over 4},{1 \over 4}} = {\Gamma\pars{1/4}\Gamma\pars{1/4} \over \Gamma\pars{1/4 + 1/4}} ={1 \over \root{\pi}}\,\Gamma^{2}\pars{1 \over 4} $$ $$\color{#00f}{\large% \int_{0}^{\infty}{\dd x \over \root{1 + x^{4}}} = {1 \over 4\root{\pi}}\,\Gamma^{2}\pars{1 \over 4}} \approx 1.85 $$
Actually, to educate the OP a little - you can use complex variables techniques here. You just have to avoid the branch points. Consider the following integral:
$$\oint_C \frac{dz}{\sqrt{1+z^4}} $$
where $C$ is the following contour:
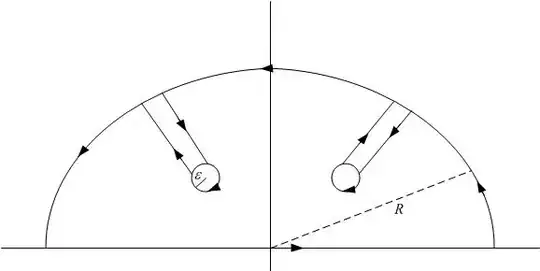
We can then write out the contour integral explicitly in terms of a parametrization; the various terms are
$$\int_{-R}^R \frac{dx}{\sqrt{1+x^4}} + i R \int_0^{\pi} d\theta \, \frac{e^{i \theta}}{\sqrt{1+R^4 e^{i 4 \theta}}} \\ + e^{i \pi/4} \int_1^{R}dt \frac{e^{i \pi/2}}{\sqrt{t^4-1}}- e^{i \pi/4} \int_1^{R}dt \frac{e^{-i \pi/2}}{\sqrt{t^4-1}}\\ + i \epsilon \int_{2 \pi}^0 d\phi \, \frac{e^{i \phi}}{\sqrt{1+(e^{i \pi/4}+\epsilon e^{i \phi})^4}} \\ + e^{i 3\pi/4} \int_1^{R}dt \frac{e^{i \pi/2}}{\sqrt{t^4-1}}- e^{i 3\pi/4} \int_1^{R}dt \frac{e^{-i \pi/2}}{\sqrt{t^4-1}}\\ + i \epsilon \int_{2 \pi}^0 d\phi \, \frac{e^{i \phi}}{\sqrt{1+(e^{i 3\pi/4}+\epsilon e^{i \phi})^4}} $$
Note that the factors of $e^{i \pi/2}$ and $e^{-i \pi/2}$ are a result of the $2 \pi$ jumps about the branch points.
In the limit as $R \to \infty$ and $\epsilon \to 0$, the second, fifth, and eighth integrals vanish. Simplifying, we are left with
$$\int_{-\infty}^{\infty} \frac{dx}{\sqrt{1+x^4}} + i 2 \left ( e^{i \pi/4} + e^{i 3 \pi/4}\right ) \int_1^{\infty} \frac{dt}{\sqrt{t^4-1}}$$
Noting that the contour integral is zero by Cauchy's theorem, we may finally deduce that
$$\int_0^{\infty} \frac{dx}{\sqrt{1+x^4}} = \sqrt{2} \int_1^{\infty} \frac{dt}{\sqrt{t^4-1}}$$
The integral on the RHS may be simplified by subbing $t=1/y$ to get
$$\sqrt{2} \int_0^1 \frac{dy}{\sqrt{1-y^4}}$$
Then sub $y = u^{1/4}$ to get
$$\frac{\sqrt{2}}{4} \int_0^1 du \, u^{-3/4} (1-u)^{-1/2}$$
which is a Beta function. Thus the integral is
$$\frac{\sqrt{2}}{4} \frac{\Gamma \left ( \frac14\right ) \Gamma \left ( \frac12\right )}{\Gamma \left ( \frac{3}{4}\right )} = \frac{4}{\sqrt{\pi}} \Gamma \left ( \frac{5}{4}\right )^2$$
The RHS may be derived using the reflection formula.
For $x \in [0,\infty]$, let $I(x)$ be the integral $\;\displaystyle\int_0^x \frac{dt}{\sqrt{1+t^4}}$.
The integral we want to calculate is simply $I(\infty)$. Quoting some results from this answer of a related question, we know for $x \in [0,\infty)$,
$$I(x) = F(\sqrt{1+x^2-\sqrt{1+x^4}}; \frac12 )$$ where $$F(y\,; m) = \int_0^y \frac{ds}{\sqrt{(1-s^2)(1-ms^2)}}$$ is the Jacobi's form of incomplete elliptic integral of the first kind.
When $x \to \infty$, $\sqrt{1 + x^2 - \sqrt{1+x^4}} \to 1$. This leads to
$$I(\infty) = K\left(\frac12\right)\quad\text{ where }\quad K(m) = \int_0^1 \frac{ds}{\sqrt{(1-s^2)(1-ms^2)}}$$ is the complete elliptic integral of the first kind. $K(m)$ can be computed efficiently using its relation with the arithmetic geometric mean of $1$ and $\sqrt{1-m}$.
$$K(m) = \frac{\pi}{2\text{AGM}(1,\sqrt{1-m})}$$
Start with $m = \frac12$, the first iteration of computing the AGM gives us
$$ \frac{1}{\sqrt[4]{2}} = \text{GM}(1,\frac{1}{\sqrt{2}} ) \le \text{AGM}(1,\frac{1}{\sqrt{2}} ) \le \text{AM}(1, \frac{1}{\sqrt{2}} ) = \frac12 (1 + \frac{1}{\sqrt{2}})$$ and hence $$ 1.840302369 \sim \frac{\sqrt{2}\pi}{\sqrt{2}+1} \le I(\infty) = K\left(\frac12\right) \le \frac{\pi}{2^{3/4}} \sim 1.868002168 $$
To get more accurate estimate of the integral, one can carry out more iterations in the AGM computation. For example, the second iteration gives us
$$ 1.854048814 \sim \frac{2^{3/2}\pi }{2^{5/4}+2^{1/2}+1} \le K\left(\frac12\right) \le \frac{\pi }{\sqrt{2^{1/4} + 2^{3/4}}} \sim 1.8541005407$$ which is accurate to about $4^{th}$ decimal places.
Mathematica input and output:
In[2]:= Integrate[1/Sqrt[1 + x^4], {x, 0, \[Infinity]}]
Out[2]= (4 Gamma[5/4]^2)/Sqrt[\[Pi]]
In[3]:= % // N
Out[3]= 1.85407
$x^2=\tan t$
$2xdx=dt/\cos^2 t$
$\displaystyle\int_0^{\infty}\dfrac{dx}{\sqrt{1+x^4}}=\int_0^{\pi/2}\dfrac{dt}{2x\cdot\cos t}=\dfrac{1}{2}\int_0^{\pi/2} \sin^{-1/2}t\cdot \cos^{-1/2}t=\dfrac{1}{4}B(\dfrac{1}{4},\dfrac{1}{4})$
The substitution $t=1/x$ leaves the integral invariant, or better, tells you that the integral from $1$ to $\infty$ equals the one from $0$ to $1$. So one way to express the answer is $$ 2\int_0^1 \frac{dx}{\sqrt{1+x^4}}=2\int_0^1\sum_{n=0}^\infty\binom{-1/2}{n}x^{4n}\,dx =\sum_{n=0}^\infty\binom{-1/2}{n}\frac2{4n+1} $$ (with a little help from Abel's theorem to evaluate the series at the edge of its convergence interval).
The series is alternating, so you get proper error estimates. But this may not be a very useful answer.
Solution using SymPy:
In [6]: from sympy import Symbol, integrate, sqrt, oo
In [7]: x = Symbol('x', real=True)
In [8]: integrate(1/sqrt(1 + x**4), (x, 0, oo))
Out[8]: gamma(1/4)**2/(4*sqrt(pi))
Despite it looks differently it is actually the same answer Mathematica gave to Julián Aguirre here:
In [9]: integrate(1/sqrt(1 + x**4), (x, 0, oo)).evalf()
Out[9]: 1.8540746773013
I just thought there might be an easy technique to estimate the integral analytically. Something like saddle point technique.
Let $t=\dfrac1{1+x^4}$ , then recognize the expression of the beta function in the new integral. Generally speaking, all integrals of the form $\displaystyle\int_0^\infty\frac{x^a}{(1+x^b)^c}dx$ can be solved this way, by letting $t=\dfrac1{1+x^b}$
