Can the following integral be computed?

Question

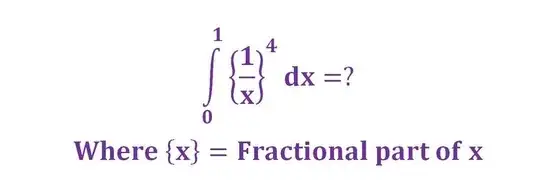
enter image description here

You can, but it is slightly messy. Divide $[0,1]$ into intervals where ${1/x}$ is continuous and has an easy expression. — Pedro, Jan 22 '14 at 05:23

score 3 · Answer 1 · answered Jan 22 '14 at 05:25

3

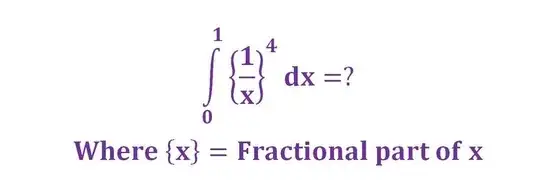
Hint: consider $$A_n=\int_{1/(n+1)}^{1/n}\{1/x\}^{4}dx$$. This can be computed. Does the series $\sum_{i=1}^\infty A_i$ converges?

answered Jan 22 '14 at 05:25

user68061

3,867

Sketch ${\frac{1}{x}}^4$ between 0 and 1. You will find that it is bounded above by a simple function. So the integral you want is bounded above by a simple integral. – Empy2 Jan 22 '14 at 06:06
please someone tell me the answer. – user121418 Jan 22 '14 at 06:23

JJacquelin · Answer 2 · 2014-01-22T12:27:31.583

1

With some preliminary transformations (in attachement) the integral is reduced to the integral of a polygamma function which is known (I let WolframAlpha do the known part of the job). enter image description here

edited Jan 22 '14 at 12:27

answered Jan 22 '14 at 12:08

JJacquelin

68,401
4
40
91

Numerical computations with Maple and Mathematica confirm the result. – Lucian Jan 22 '14 at 19:23

Lucian · Answer 3 · 2014-01-22T11:34:58.413

First, let's prove that it converges:

$$\int_0^1\bigg\{\frac1x\bigg\}^4dx=\int_1^\infty\frac{\{t\}^4}{t^2}dt\color{red}<\int_1^\infty\frac{1^4}{t^2}dt=\bigg[-\frac1t\bigg]_1^\infty=1,\qquad\text{since }0\le\{t\}<1.$$

$$\int_0^1\bigg\{\frac1x\bigg\}^4dx=\int_1^\infty\frac{\{t\}^4}{t^2}dt=\sum_1^\infty\int_k^{k+1}\frac{(t-k)^4}{t^2}dt=\sum_1^\infty\int_0^1\frac{u^4}{(u+k)^2}du=$$

$$=\sum_1^\infty\bigg(\frac43-2k+4k^2-\frac1{k+1}+4k^3\ln\frac k{k+1}\bigg)=\ldots<1$$

Can the following integral be computed?

3 Answers3