Splitting a sandwich and not feeling deceived

Question

This is a problem that has haunted me for more than a decade. Not all the time - but from time to time, and always on windy or rainy days, it suddenly reappears in my mind, stares at me for half an hour to an hour, and then just grins at me, and whispers whole day: "You will never solve me..."

Please save me from this torturer.

Here it is:

Let's say there are two people and a sandwich. They want to share the sandwich, but they don't trust each other. However, they found the way how both of them will have a lunch without feeling deceived: One of them will cut the sandwich in two halves, and another will choose which half will be his. Fair, right?

Split sandwich

The problem is:

Is there such mechanism for three people and a sandwich?

EDIT: This was roller-coaster for me. Now, it turns out that there are at least two books devoted exclusively on this problem and its variations:

Fair Division

Cake Cutting Algorithms

Books on fair division

Yesterday, I was in a coffee shop in a small company. We ordered coffee and some chocolate cakes. As I was cutting my cake for my first bite, I felt sweat on my forehead. I thought, 'What if some of my buddies just interrupt me and say: Stop! You are not cutting the cake in a fair manner!' My hands started shaking in fear of that. But, no, nothing happened, fortunately.

Yes, see Wikipedia: Category:Fair division and in particular Selfridge–Conway — Chris Culter, Jan 14 '14 at 05:20
Brams and Taylor have an envy-free procedure for more than three people. (See my answer below.) You are a free man again. — JRN, Jan 14 '14 at 08:01
Since we are in mathematics, we might want to apply the Banach–Tarski paradox N-1 times to solve the problem for N people... — PlasmaHH, Jan 14 '14 at 10:57
This seems trivial. Each person rolls dice. The low score cuts the sandwhich into portions. Then each participant chooses a single portion according to highest dice order. Now since the cutter chooses last, he will obtain the smallest portion, as in the case with 2 participants, but it is clear that the number of participants do not matter. Therefore, he will maximize the size of the smallest portion. But this must mean that all portions are equal. Am I missing something here? — Paul, Jan 14 '14 at 11:01
I wonder if anyone has ever looked into a Dictator Game-based stochastic variation. In experiments with things like Dictator Game, people tend to reject unfair offers, even if it makes them uniformly worse off. That is, they are usually willing to pay some "fairness premium" and simply deny any form of splitting the resources unless they are equal to or better than all of the other players. If we assume humans will use this heuristic, then we could take any N pieces of a divided sandwich and randomly assign them to people in a Dictator Game, where the "worst-off" person is the dictator. — ely, Jan 14 '14 at 18:45
Thus, anyone cutting pieces has an incentive to make sure the worst off piece is at least good enough that whoever randomly draws it will decide to keep it, so that everyone gets to keep theirs too. My guess is this leads to some Nash equilibrium kind of thing where making equal cuts leads to the highest expected value. — ely, Jan 14 '14 at 18:47
@paul your algorithm assumes that the players agree on which pieces are bigger than each other. The problem becomes nontrivial when you remove that assumption. If A cuts the cake, then A will believe all three pieces are equal. Then B takes a piece-but if C disagrees with A and believes B's piece is bigger than the others, the solution isn't envy-free. That's the beauty of the Selfridge-Conway procedure: all three players are guaranteed to believe they got a fair slice. — Kevin Carlson, Jan 14 '14 at 22:00
@Paul That procedure is not coalition-resistant. After the players have rolled, the cutter can make the following offer to the first chooser "I will make no cuts, then you can choose the entire cake, and we shall split it among ourselves." This leaves the other $n-2$ players empty handed. — in_mathematica_we_trust, Jan 15 '14 at 10:04
@in_wolfram_we_trust Ah, but that collusion is not subgame perfect. Or, in less technical terms, you need an enforcement mechanism in case there is no honor among thieves. The cutter does have a knife :-) Also, it can be a repeated game. Or, there can be things that can happen externally. But if the cutter can't trust the person who gets the big piece, then there is no way to collude. — Paul, Jan 15 '14 at 10:07
This seems to be a duplicate of http://math.stackexchange.com/q/2450/119592 — Bernd, Jan 16 '14 at 12:27
The fairest thing is for the person who cuts to pick last. Unless they are working in cahoots with the person who picks first it is in their best interest to cut as evenly as possible. — 0xFADE, Jan 16 '14 at 21:27
Upvoted for the bibliography: One will cut and the other will choose is my dad's favourite since I have memory :) — MattAllegro, May 12 '14 at 22:27
fyi heres a neat recent NYT article on the subj, nice to see abstract subj covered in the MSM... To Divide the Rent, Start With a Triangle — vzn, Jul 24 '14 at 23:15
@MichaelGreinecker: More than 380 people disagree with you. Democratically, even if it wasn't a math question, it has been voted to be one, now. — Nick, Sep 30 '14 at 07:57
Doesn't the same logic apply? Have one cut, and the other two can choose. The cutter is not going to make any piece larger than the other two pieces because he gets last pick. — JobHunter69, Dec 05 '16 at 05:41
A fair division can be anything from any one's perspective. An extreme, but very common example. Dividing a sandwich between three starving people means they all die of starvation, unless one gets 100% and lives and the rest get 0% and die. For each person the fair division is if he gets 100%. Another extreme example is when none of the 3 like sandwiches. Mathematical solution is only possible when "fair" can be formally defined, but it can hardly be because it is subjective. I.e. each person has his own definition of fairness. So it can only be approximated at best — Arthur Tarasov, Oct 05 '18 at 04:40
Slightly unrelated comment: I'm a simple guy, I cut the sandwich and give my brother the smaller part. I'm happy, he is happy too as he doesn't know. — , Nov 12 '19 at 19:03
I am late to the sandwich party, but there's the Gale-Shapley Algorithm (see: https://en.wikipedia.org/wiki/Gale%E2%80%93Shapley_algorithm). Any one can make the cuts (perhaps use the moving knife protocol). Each piece is numbered and the participants are assigned numbers at random. The participants also make their secret number selection. Then run the Gale Shapley algorithm to get optimal assignments. Its proven to be optimal and assignments are stable. — vvg, Sep 26 '20 at 00:33
This situation just came up for me today. I had to share a sandwich with my brother. My brother got the knife first, so to save myself from getting scammed, I suggested that my brother cut the sandwich and that I get to pick the piece. This would make sure that my brother cuts the pieces equally to make sure I don't get too much of the sandwich. However, he realized that cutting the sandwich equally is extremely difficult and that the cutter is at an automatic disadvantage. So we argued about who would cut the sandwich until I gave in and cut the sandwich. I got the smaller piece. — Some Guy, Oct 05 '22 at 00:51

score 287 · Answer 1 · answered Jan 14 '14 at 05:42

287

For more than two, the moving knife is a nice solution. Somebody takes a knife and moves it slowly across the sandwich. Any player may say "cut". At that moment, the sandwich is cut and the piece given to the one who said "cut". As he has said that is an acceptable piece, he believes he has at least $\frac 1n$ of the sandwich. The rest have asserted (by not saying "cut") that is it at most $\frac 1n$ of the sandwich, so the average available is now at least their share. Recurse.

answered Jan 14 '14 at 05:42

Ross Millikan

383,099

23

Note that this is not an envy-free division but just called a proportional division. In fact there is an easy solution for that that doesn't require a moving knife (https://en.wikipedia.org/wiki/Proportional_%28fair_division%29). Some people will not think a moving knife algorithm is fair because the one moving the knife may move slightly after someone says "Cut!". – user21820 Jan 14 '14 at 05:43
Ok, than because of that lag, Chris Culter's solution from Wikipedia will be accepted as answer, but this answer is also clever and interesting. – VividD Jan 14 '14 at 05:47
109

Nice! You used the invisible hand of the market to cut the sandwich. – user Jan 14 '14 at 10:29
12

@user One could build a machine and everyone gets a button. Not exactly ideal for a student flat, unless they are engineering students... – user1729 Jan 14 '14 at 11:29
31

@user1729 Engineering students would design the machine to ensure accurate proportioning to start with, you'd only need one button to start the machine (and to stop it, for safety reasons). – JAB Jan 14 '14 at 12:55
2

@JAB You have too much faith in Engineers - my boss is an engineer, and he doesn't even keep a screw-driver in his office! – user1729 Jan 14 '14 at 13:00
@user1729 Engineering students, not graduated engineers. It'd be their final design project. – JAB Jan 14 '14 at 13:22
2

You are describing a Dutch auction. This works well and is still in use in the marketplace. – Torben Gundtofte-Bruun Jan 14 '14 at 15:37
7

@user1729 then your boss is not an engineer. He just thinks he is. – John Jan 14 '14 at 18:14
2

@VividD I don't think this one is coalition resistant either xD. Player 2 and 3 can agree to never call cut until a sliver off the end, and split their big piece in half. – Cruncher Jan 14 '14 at 19:39
@Cruncher: If 2 and 3 agree this and 1 knows about it, he can claim 1/2 (or more) and leave 2 and 3 to split the other half. – Ross Millikan Jan 14 '14 at 20:43
3

@Cruncher, even if 1 does not know about it, he can call cut anytime after 33% to get the biggest piece – pho Jan 14 '14 at 23:45
3

I would lose more weight because of suspense of the procedure than I would gain by eating my part of the sandwich. – VividD Jan 15 '14 at 00:27
2

A quibble: you say "Recurse," but, since only the "remaining" (presumably larger) piece is subject to further cutting, I believe that this is iteration. – Scott - Слава Україні Jan 15 '14 at 00:53
@Scott: Fair enough. – Ross Millikan Jan 15 '14 at 01:06
2

@Scott It's iteration if it's event-based, function cut() is called n times... but if you have cut(remainingpiece, user) that subtracts, waits and calls itself when appropriate, that would be recursion. – NoBugs Jan 15 '14 at 02:47
2

If ALL people want all of the cake, one would "cut" after most was selected, making this very unfair. – NoBugs Jan 15 '14 at 02:49
3

@NoBugs each thought the risk was worth it (to wait for a chance at a bigger piece), because each could have claimed the first 1/3 of the sandwich. – Yakk Jan 15 '14 at 14:55
@NoBugs ah, the tragedy of the commons.... – o0'. Jan 15 '14 at 15:53
3

Not sure why this choice is getting so many up-votes. It is not envy-free, and it does not particularly ensure an even split. In fact, the author himself says that the first person believes he has AT LEAST 1/nth of the sandwich. This implicitly guarantees that the remaining folks have AT MOST 1/nth of the sandwich. The likelihood, especially after doing this twice over, of everyone getting 1/nth is low. In fact, I can imagine my kids complaining that this just ensures the kid with the quickest / loudest mouth gets the largest piece. – Mike Williamson Jan 15 '14 at 17:41
@NoBugs Iteration can always be couched as recursion; e.g., work_a_series_of_days(n) { work(n); if (n != Friday) work_a_series_of_days(n+1); } But calling an essentially iterative process recursive is just confusing and adds unnecessary complexity. I don’t understand your comment, but note that, if there are n people, then the cut function will be called n – 1 times. – Scott - Слава Україні Jan 15 '14 at 21:58
2

@MikeWilliamson This question is not about equal division by an absolute standard (e.g., mass); it’s partly about perception. If one person gets all the bacon, another gets all the lettuce, and a third gets all the tomato, they might all feel that they got the best deal. So, please describe your non-envy-free scenario precisely. ... (continued) – Scott - Слава Україні Jan 15 '14 at 22:11
1

@MikeWilliamson (continued) Note that anybody can say “cut” at any time. For the first person to be able to say “cut” when he does, the other n – 1 must have remained silent, indicating that they felt that the first piece is still ≤ 1/n, and so the remaining piece is still AT LEAST (n-1)/n of the sandwich. The key is that the person with the knife moves it slowly enough that this doesn’t just reduce to a quickest mouth contest. – Scott - Слава Україні Jan 15 '14 at 22:12
3

@MikeWilliamson: we were not asked for envy-free. We were asked to find a way that each person (by his behavior) has asserted that he got at least $\frac 1n$. I have seen the (much more complicated) approaches to envy-free but think this is a useful approach. – Ross Millikan Jan 15 '14 at 22:15
2

Great! This also ensures that it's cut in exactly 3 pieces! – Viktor Mellgren Jan 16 '14 at 23:07
@Scott Exactly - like how Haskell has no for loops. – NoBugs Jan 18 '14 at 06:12
Okay if more than one yells at the same time, the knife goes back to the start and they try again. This solves the yellers' tie-break but won't solve the knifer's lag. – user21820 Jan 23 '14 at 01:27

score 270 · Accepted Answer · edited Jul 13 '14 at 01:08

270

Just for the record, here's the Selfridge–Conway discrete procedure mentioned in the comments. The Wikipedia article also contains some commentary on its origin and why it works.

This procedure was the first envy-free discrete procedure devised for three players. The maximal number of cuts in the procedure is five. The pieces are not always contiguous. Solutions for n players were also found later.

Suppose we have three players P1, P2 and P3. Where the procedure gives a criterion for a decision it means that criterion gives an optimum choice for the player.

Step 1. P1 divides the cake into three pieces he considers of equal size.

Step 2. Let's call A the largest piece according to P2.

Step 3. P2 cuts off a bit of A to make it the same size as the second largest. Now A is divided into:

the trimmed piece A1

the trimmings A2.

Leave the trimmings A2 to one side. If P2 thinks that the two largest parts are equal, then each player chooses a part in this order: P3, P2 and finally P1.

Step 4. P3 chooses a piece among A1 and the two other pieces.

Step 5. P2 chooses a piece with the limitation that if P3 didn't choose A1, P2 must choose it.

Step 6. P1 chooses the last piece leaving just the trimmings A2 to be divided.

Now, the cake minus the trimmings A2 has been divided in an envy free manner. The trimmed piece A1 has been chosen by either P2 or P3. Let's call the player who chose it PA and the other one Player PB.

Step 7. PB cuts A2 into three equal pieces.

Step 8. PA chooses a piece of A2 - we name it A2₁.

Step 9. P1 chooses a piece of A2 - we name it A2₂.

Step 10. PB chooses the last remaining piece of A2 - we name it A2₃.

Wikipedia on the origins this procedure:

This procedure is named after John Selfridge and John Horton Conway. Selfridge discovered it in 1960, and told it to Richard Guy, who told it to many people, but Selfridge did not publish it. John Conway discovered it independently in 1993, and also never published it, but the result is attributed to them in a number of books.

edited Jul 13 '14 at 01:08

VividD

16,196

answered Jan 14 '14 at 05:44

Chris Culter

27,415

35

this method is envy-free, @Chris Culter, but is it coalition-resistant? – VividD Jan 14 '14 at 18:10
1

@VividD, yes it is. It's easy to see if you read the analysis in the end of the wikipedia articles. – Andrew Savinykh Jan 14 '14 at 20:28
460

This answer is no good. It refers to cutting up a cake, whereas the question is clearly about cutting sandwiches. – AviD Jan 14 '14 at 22:16
7

There is a difference between cutting a cake and cutting a pie. From Science News:
Mathematicians simplify cake cutting by assuming that all slices are perpendicular to one particular side of a rectangular cake, with no crosswise cuts. Following that rule, there is only one way to split a rectangular cake into two equal-size pieces.

For a pie, however, there are an infinite number of ways, because there an infinite number of lines going through the center of a circle.
– JRN Jan 14 '14 at 23:37
So how does this method account for equally distributed contents? Round meat anyone? I always plan on picking the middle piece! – Mottie Jan 15 '14 at 13:36
9

@Mottie It handles it well. Each player divides the sandwich into equally valued pieces from their perspective. If they value meat more, pieces with meat should be smaller than pieces with less meat. If they don't care about bread at all, then they can just cut the meat up evenly, and ignore the amount of bread in each piece. The big downside is incompetence: in the two-player game, it is almost always a better idea to be the 2nd player than the 1st, because it is easier to determine which of two pieces are bigger than it is to cut something into two even pieces. – Yakk Jan 15 '14 at 14:52
I really don't see why one person A would create 3 equally valued pieces by doing two cuts.. That's the entire source of the problem! The one doing the cutting is not necessary unbiased over which cut is better... Besides, who values trimmings on a sandwich as highly as an unbroken slice anyway ;) – Spork Jan 15 '14 at 16:22
Does this become recursive with the trimmings? "leaving just the trimmings A2 to be divided" – Luke Jan 15 '14 at 19:44
@Yakk what if people have different value on meat versus potatoes? – corsiKa Jan 15 '14 at 20:10
@Luke No, at least according to Wikipedia's analysis; the protocol terminates where indicated. – Chris Culter Jan 15 '14 at 20:13
@corsiKa if you play "honestly", you will always pick something that is "at or above average" from your own perspective. If you take into account opponent's perspectives, and they play "honestly", they will still get something "at or above average" as far as they are concerned, and so will you. If you play based on their preferences, and they play tit-for-tat to punish it, they could take something that is above average for their preferences yet force you to take something that is below average for your preferences in some cases. But that is the cost of meta gaming (you left yourself open) – Yakk Jan 15 '14 at 22:12
Cake cutting algorithms work best where people's utility functions are very different (they like different things). I once tried a 5 person (not envy free that would have been too hard) division algorithm with some colleagues in Cambridge University Computer Laboratory and some cakes I had bought from a local shop. We all ended up happy and there was a cake left over (which none of us like - and was eaten by a 6th passer-by) :-) It is certainly worth trying this out. – Francis Davey Jan 16 '14 at 20:47
One problem is that it generates more than 3 pieces (If the division is not correct from the beginning) And I wouln't want 1 piece + small scraps – Viktor Mellgren Jan 16 '14 at 23:12
@AviD Good observation (y) – Prakash Vishwakarma Jan 17 '14 at 05:14
PB cuts A2 into three equal pieces. ?? then why cant A1 cut the cake that way(at first place) or pass the knife to A2. – ratan kumar Jan 18 '14 at 12:22
1

If one let's the part until people start eating the trimmings be "!", and the rest be "@", then one could just repeat ! for the trimmings and so on until any one of them die, so they wouldn't car abzout sandwitches any longer. – Abhimanyu Pallavi Sudhir Jan 18 '14 at 14:01
But what if P2 doesn't care, and cheats while cutting off a bit of his "largest piece"? Or what if everyone wants the same tomato? – Abhimanyu Pallavi Sudhir Jan 18 '14 at 14:02
A great theoretical answer of limited practical use. :^) This cake will be little more than crumbs by the time it is divided up. You'd better have an awfully sharp knife. – J.R. Jan 20 '14 at 12:57
http://i.imgur.com/j74SykU.gif – Adsy Jan 22 '14 at 17:13
@AviD how can you get more pivoted than the answer itself ? :O – PleaseHelp Oct 24 '14 at 18:35

score 73 · Answer 3 · answered Jan 14 '14 at 08:08

73

For dividing a cake to $n$ people, there is an algorithm that guarantees that:

Each of the $n$ people gets a piece that he considers at least as good as each of the other pieces (i.e., the division is envy free);
All pieces are connected (actually, all pieces are rectangles).

This algorithm was invented by Forest Simmons and published by Francis Su at 1999.

The only problem with this algorithm is that its runtime is not bounded, i.e., it might take forever (As proved by Stromquist at 2008, no bounded algorithm can find an envy-free division when we want the pieces to be connected).

But, you can stop at any time and get a division that is approximately envy free.

answered Jan 14 '14 at 08:08

Erel Segal-Halevi

11,509

3

Great answer, explains high-level facts about the algorithm. – VividD Jan 14 '14 at 17:35
17

Still, this is basically a link-only answer, since it doesn't even give an hint on how the actual algorithm works. – o0'. Jan 15 '14 at 15:54
What about the auction-style algorithm ? One player moves the knife over the surface. When it appears to have covered 1/n of the cake, he continues moving until a person calls out stop. When they do, he cuts the cake at that point. The player who called out stop takes the cut portion. This continues till the cake is divided. – William Grannis Mar 06 '18 at 21:11
@William Grannis: This solution is the one Ross Millilan referenced, the problem with (implementing) it in practice is that it is continuous-time based. – Vandermonde May 03 '20 at 18:09

Briguy37 · Answer 4 · 2014-01-15T16:09:43.903

Here's a variation on the accepted answer.

A cuts the sandwich into 3 parts
If B thinks the top 2 pieces are equal
  C chooses a piece
  B chooses a piece
  A gets the remaining piece
Else
  B re-balances the 2 biggest pieces.
  C chooses a piece
  If only one of B's re-balanced pieces remain
    B gets that piece
    A gets the remaining piece
  else
    A chooses a piece
    B gets the remaining piece

Summary:

A will get one of their original "equal" pieces or more, and is thus happy.
B will get one of the pieces they adjusted, and are thus happy.
C will get first choice, and is thus happy.
Although each person should get at least a third in their mind, this doesn't qualify as an envy-free solution. For example, if B re-balances two pieces and C chooses the piece B increased, then A would envy C because he got more than 1/3 in A's mind. However, A still gets 1/3 in their mind.

I think you can generalize this pattern for $N$ people. Simplified, you give up your place in the picking order if you rebalance, but the trade-off is that you are guaranteed to get a piece you rebalanced or a bigger one. Here's a first take at the priority rules for the picking procedure, though I'm not sure it handles all cases:

If N people each have N pieces they rebalanced remaining, the first person who rebalanced from that group gets to choose from their rebalanced pieces. For example, if there is one piece left from the pieces you re-balanced, you get that piece.
If you did not re-balance, the highest number gets to pick first
If you did rebalance, the lowest cutter gets to pick first

Also, here's an example of how it would work for 4 people:

A cuts the sandwich into 4 equal pieces
If B thinks the top 3 pieces are equal:
  If C thinks the top 2 pieces are equal:
    D chooses a piece
    C chooses a piece
    B chooses a piece
    A gets the last piece
  Else:
    C rebalances the top 2 pieces
    D chooses a piece
    If only one of C's rebalanced pieces remain:
      C gets the other rebalanced piece
      B chooses a piece
      A gets the last piece
    Else:
      B chooses a piece
      If only one of C's rebalanced pieces remain
        C gets the other rebalanced piece
        A gets the remaining piece
      Else
        A chooses
        C gets the remaining piece
Else:
  B rebalances the top 3 pieces
  If C thinks the top 2 pieces are equal:
    D chooses a piece
    C chooses a piece
    If only one of B's rebalanced pieces remain:
      B takes that piece
      A gets the final piece
    Else:
      A chooses a piece
      B gets the final piece
  Else:
    C rebalances the top 2 pieces
    D chooses a piece
    If only one of C's rebalanced pieces remain:
      C gets that piece
      If only one of B's rebalanced pieces remain:
        B gets that piece
        A gets the last piece
      Else:
        A chooses a piece
        B gets the other piece
    Else if only 2 pieces rebalanced by both C & B are left:
      B chooses one of the rebalanced pieces
      C gets the other one
      A gets the last piece
    Else:
      A chooses a piece
      If only one of C's rebalanced pieces remain:
        C gets that piece
        B gets the final piece
      Else:
        B gets to choose
        C gets the final piece

@AndrewLarsson: No, A will always get one of his fair pieces or more. — Briguy37, Jan 15 '14 at 02:42
Oh, for some reason I read your answer incorrectly. Your answer is actually the best one so far. I like it much better than the accepted answer. — Andrew Larsson, Jan 15 '14 at 02:49
One problem is the rebalancing, I personally wouldn't want a sandwich that is almost 1/3 + several small pieces of sandwich — Viktor Mellgren, Jan 16 '14 at 23:06
@Vixen, this could be solved by A only cutting out 1/3 and leaving B to cut the remaining piece in to two parts, after that the algorithm is the same. — Craig, Jan 20 '14 at 10:15
@Vixen One way around that is to have everyone mark where they would make their cuts and only actually make them when everything is final. However, unless you have a machine doing the cutting, you'd have to do the final cuts in order by the time they were suggested and by the person who suggested them, and fallback to the original algorithm if anyone down the line thinks a previous cutter made a different cut than they originally suggested. — Briguy37, Jul 22 '14 at 15:24

user68061 · Answer 5 · 2014-01-14T11:31:09.377

Okay, so this is just a small comment about the "general science'' behind all these. You can understand a sandwich as a measure space with $n$ given measures. Also, these measures are non-atomic, otherwise you can not solve the problem even for two people. These measures generate a vector measure on the ``sandwich''. Now you can apply Lyapunov theorem and say, that the range of this measure is closed and convex. But the points $(1,1,...,1)$ and $(0,0,...,0)$ lie in the range, thus the point $(1/n,..., 1/n)$ does. This means, that there is a piece of sandwich such that each person thinks that it is exactly $1/n$ of the whole sandwich. Now you can give it to anyone and repeat the procedure. Cool thing is that you will divide the sandwich in such a way that each person will think, that the sandwich is divided into equal parts. So one can solve the problem in the following form "There is a way to divide a sandwich such that each person thinks that no one have more sandwich than him". I have no idea how to make an explicit algorithm for that one.

To elaborate on the unsolvability of the problem for atomic measures: If all measures assign measure $1$ to a given point, there is only one winner. In other words, if there is an indivisible "cherry" on the cake that everyone wants, only one person can get it and the rest will be unsatisfied. — Mario Carneiro, Jul 08 '16 at 00:52

score 29 · Answer 6 · answered Jan 14 '14 at 07:16

29

According to Wikipedia, the Brams-Taylor procedure is

the first finite procedure to produce an envy-free division of an infinitely divisible good among any positive integer number of players.

A nice discussion about it can be found here.

answered Jan 14 '14 at 07:16

JRN

6,691

38

Ironically it is patented instead of infinitely copied and shared in an envy-free way with the n players of the internet... – Chris Wesseling Jan 14 '14 at 13:32
5

@ChrisWesseling I'm going to patent the method for taking into account the overhead costs of paying a royalty every time you use this method to determining whether you would be better off using it versus luck or fend for yourself. – Michael Jan 14 '14 at 15:26

pwned · Answer 7 · 2014-12-16T17:50:56.793

25

Nobody said it has to be a discrete process. Just blend the sandwich into infinitestimally small pieces, everyone eats small pieces at the same speed until there is nothing left. Lucky person gets to lick the blades.

edited Dec 16 '14 at 17:50

answered Jan 14 '14 at 12:33

pwned

447
6
11

6

"until they ate a third of the mess." How do you decide when that happens? – Dan Hulme Jan 14 '14 at 14:19
7

I believe it will naturally happen when the sandwich ends, if each person eats 1 piece at a time. – Conrad Clark Jan 14 '14 at 15:07
1

@DanHulme fixed – pwned Dec 16 '14 at 17:51
3

the trust problem is not solved. it will end as a speed eating competition. plus, the sandwich will be eaten infinitesimally fast, losing the benifit of taste (texture was already eliminated by blending). but,i have to admit, the solution adds much fun and adrenalin. – user160823 Aug 12 '16 at 03:37

John U · Answer 8 · 2014-01-14T05:45:04.610

24

Complete EDIT (too lazy to formulate mathematically): Imagine X as a sandwich just for simplicity. The first person cuts X into thirds "horizontally" and they have to cut across the whole sandwich in a straight line with each cut. The second person cuts each third into thirds by cutting the sandwich "vertically" with each cut going through all of the original thirds in a straight line. Now there are 9 pieces. Third player picks one piece and then first person picks, then second and third again in a circle.... This operation with the horizontal and vertical constraints (and having to go right across the sandwich) should avoid anyone feeling deceived.

edited Jan 14 '14 at 05:45

answered Jan 14 '14 at 05:15

John U

400

11

Of course if it was an actual sandwich it would be destroyed probably by cutting it into 27 pieces :) – John U Jan 14 '14 at 05:17
I know there is the known solution posted in the OP comments - I just feel there should be multiple ways to achieve this and I already started thinking about it :) – John U Jan 14 '14 at 05:37
2

I am upvoting this solution because of its 3D nature. :) – VividD Jan 14 '14 at 05:37
7

So, for four people we would need sandwich in 4-dimensional space? ;) – VividD Jan 14 '14 at 05:38
Haha.. no.. we could formulate the "edited" part so it works I think for any number of people by constraining the way the subsequent person "cuts" so that some kind of ratios are maintained. Would not be hard to formulate and indeed this has intrigued me. It still might be wrong so I may try and formulate and generalise (its probably known also). Surely there are more ways to solve this problem though - depending on how much you want to mangle the sandwich :). – John U Jan 14 '14 at 05:43
1

Well imposing the ratios is just as difficult (if not more, what with all the crumbs) than just requiring one of the three to divide fairly. Furthermore even imposing ratios doesn't solve the problem because some parts of the sandwich may be mouldy... – user21820 Jan 14 '14 at 05:52
The difficulty of enforcing the ratios depends on the problem I think.. if we think of just a piece of paper and cutting as drawing lines to divide the paper into rectangles (whose area as a percentage of the whole paper represents the division of the wealth of El Dorado to make it interesting) then enforcing the required ratios is just a matter of enforcing lines to be drawn horizontally and vertically (no matter how many people are involved).. – John U Jan 14 '14 at 06:35
@JohnU This is why a common version of this problem involves gold diggers or bandits, and a sack of gold powder. – vsz Jan 14 '14 at 07:27
2

You are assuming much too much about the 'uniformity' of the value ascribed to areas of the sandwich. – jwg Jan 14 '14 at 13:14
1

@JohnU: Ah but I don't trust others to draw straight lines, not to say parallel to an axis! I can't even do it myself; my ruler is never perfectly straight. Then again, I would have volunteered to be envy-free so that the others would be happy with their piece of bread. – user21820 Jan 14 '14 at 13:36
horizontally/vertically = I think you mean to say that the first divisions are in a North/South direction and the next cuts are East/West direction, right? You don't really mean to cut a sandwich in the direction parallel to the table surface (unless the table is at 90 degree angle to the floot (unless the floor is at 90 degree angle to the house (unless the house is at 90 degree angle to GRAVITY)? – Torben Gundtofte-Bruun Jan 15 '14 at 07:26
can you give any intuition about why this might work? – user160823 Aug 12 '16 at 03:42

score 24 · Answer 9 · edited Jul 11 '14 at 05:04

24

From You cut I choose:

An interesting solution is outlined in "Mutiny on the H.M.S. Bounty", called the Who-shall-have-this Method. Say there are $N$ people to divide between, they choose from amongst themselves two people - $A$ and $B$. $A$ stands where $B$ cannot observe him, and divides the cake. B then points to someone and that someone comes to claim his share of the cake. $B$ may at any time point to $A$ or to himself, but since he never can see which segment of cake he's giving out, and since $B$ and $A$ are both chosen by the crowd, there is virtually no opportunity for intentional collusion.

This method still won't guarantee everyone a satisfactory cut of the cake, but it gives $A$ the correct motivation, since only by dividing the cake evenly can he hope to get a large piece for himself.

edited Jul 11 '14 at 05:04

VividD

16,196

answered Jan 14 '14 at 16:34

Nancy Hastings-Trew

365

I think I like this method the best so far, even better than the solution I proposed. – Kevin Fegan Jan 14 '14 at 21:20
This method really has some appeal. @Nancy Hastings-Trew : I maybe don't fully understand it. Does this mean that A cuts the cake in N peaces? And that B repeatedly points to next person who in turn chooses his/her share? – VividD Jan 15 '14 at 17:30
@Kevin Fegan, is my interpretation in my previous comment correct? – VividD Jan 15 '14 at 18:18
1

@VividD Yes, I believe so. A cuts all pieces the same so that if he is pointed to last, he still gets 1/n of the cake. However, this still has the same flaw as the "You Cut I Choose" method, in which A cannot plan to receive more than 1/n of the cake, while the first person chosen is guaranteed more than 1/n (because no one can cut cake that evenly). – Timtech Jan 15 '14 at 22:08
I think it's interesting that, according to Bligh, this method was well-known and often practiced, at least among sailors of the time. His account mentions several birds divided this way: “The bird was about this size of a small pigeon. I divided it, with its entrails, into eighteen portions, and by a well-known method at sea, of, Who shall have this? it was distributed…” But he doesn't explain the method, leaving one to suppose that it was well-known even by people who weren't sailors. – MJD Jan 16 '14 at 17:29
It would be wonderful if a group of pirates were using this Who shall have this? method, and A, the one dividing the loot, intentionally divided it into unequal portions. Not to try to get a larger share for himself, since that obviously wouldn't work, but to start a fight so that he might stage a mutiny and take over the ship. :) – David Conrad Jan 16 '14 at 18:53
2

@Timtech - "... while the first person chosen is guaranteed more than 1/n (because no one can cut cake that evenly". It's assumed that A will attempt to cut the cake as evenly as possible (of course, there will be some variation). But, the first piece A chooses to distribute will not necessarily be the biggest. A will just start at some "random" point for the first piece, so there is no guarantee that the first person chosen will get a piece that is larger than 1/n. If this was somehow guaranteed, then B would always choose himself first to be guaranteed a bigger piece. – Kevin Fegan Jan 16 '14 at 20:08
1

@VividD - your interpretation is close... A first divides the cake to allow for a piece for everyone, and then selects a piece to be distributed. B selects a person to receive the selected piece, but B can't see the piece that A selected. The selected person must accept the piece that A selected. A then selects the next piece, and so on. – Kevin Fegan Jan 16 '14 at 20:29
But if A is willing to accept the a small risk of getting a small piece in exchange for a larger chance of getting a large piece, then A may in fact cut a small number of very small pieces, which are unlikely to be his, in order to make the remaining pieces larger. – John Robertson Mar 04 '14 at 06:25

score 16 · Answer 10 · answered Jan 14 '14 at 05:48

16

This was covered in the first class I ever TAed in graduate school. Naturally, the reaction of most of the students was, "why don't they just eat the cake?"

Person A cuts it into two pieces she views as "of equal value." Person B then chooses her favorite half. A and B then each divide their halves into thirds that they views as "of equal value." Person C then chooses her 1 favorite piece from A and one favorite piece from B. This ensures a fair (but not envy-free) division.

answered Jan 14 '14 at 05:48

Nick D.

2,464

Yes this is the inefficient solution in the Wikipedia article I gave. The other solution there takes a polynomial number of cuts which comes up to only 3 cuts for 3 people. – user21820 Jan 14 '14 at 05:55
1

I like this version for its simplicity. The general recursive algorithm: if $n = 1$ then take the whole cake; if $n > 1$ then recursively divide the cake among $n-1$ people and then have each of those people divide their cake into $n$ portions they believe are equal. The $n$-th person now chooses one portion from each of the $n-1$ other people. – ntc2 Jan 16 '14 at 21:51

score 16 · Answer 11 · answered Jan 14 '14 at 20:40

16

Divide the sandwich into three portions and weigh each one on a digital scale. Adjust until the portions are the same. If equal distribution of condiments is a point of contention, the sandwich must be pureed prior to portioning. No one said it had to taste good.

answered Jan 14 '14 at 20:40

egbrad

285

1

Amusing to say the least. – Vladhagen Jan 14 '14 at 21:07
3

Perhaps we need an entropy measure of the resulting condiment distributions to quantify the tolerance of our eaters to condiment envy risk ;) – bright-star Jan 15 '14 at 07:05

user160823 · Answer 12 · 2023-07-05T05:44:51.233

15

My professor for Game Theory asked me this question,and I gave him an answer that he said that is the simplest he had ever heard (also Steaven Brhams said it's nice):

P1 divides the cake to 3.
P2 notes the smallest,in his opinion; let it be A.
If P3 wants A, let him have it.
Else P1 takes it, and we have only 2 which we know how to solve.

edited Jul 05 '23 at 05:44

answered Jul 29 '14 at 06:53

user160823

730
6
14

Sorry for the super late comment, but suppose that P3 does not want the piece. Then P1 takes it. So P1 is out of consideration for future pieces. THen how do P2 and P3 decide who gets which of the remaining pieces? – Joe Sjoberg Sep 18 '19 at 14:52
@JoeSjoberg I fixed that in my edit – Ekadh Singh Jan 06 '20 at 19:01
@JoeSjoberg either they agree, or just cut each of them to 2, as mentioned in the question. – user160823 Jul 05 '23 at 05:45

bright-star · Answer 13 · 2014-01-14T08:10:13.083

14

Okay, I've got a weird idea that I think might work.

Viewed from above, the sandwich is a square, right? Since a square is technically a disc in $L_1$ space, I think you can use the pizza theorem to cut it into 12 pieces and divide it evenly with way less work than Selfridge-Conway.

I think this should work because 12 divides into 4 (a pizza theorem requirement) but also divides into 3. I started with the following image from Wikipedia:

Pizza theorem for 12 slices

My algorithm was, first divide the pizza along the cardinal directions. Then, enumerating over each such section, color each first wedge, second wedge, third wedge, and fourth wedge (modulo 3) black. Offset that sequence by 1, and repeat twice more. Here is the result:

I have a feeling that this is at least a good approximation. The color permutation might not be so simple, though--the claim is that there exists such a permutation for any set of cuts that satisfy the requirements of the theorem.

edit: I'm more confident about this one.

The algorithm for this one is much more intuitive:

Observe that there are 3 "opposite pairs" of slices of each color.
Select one opposite pair of each color, and recolor it.

Possible solution for 3 people

The claim is that each pair of opposites is a third of half of the ~~pizza~~ sandwich.

edited Jan 14 '14 at 08:10

answered Jan 14 '14 at 07:03

bright-star

1,171

6

Disclaimer: This may only work on square circles in a Manhattan world ;) – bright-star Jan 14 '14 at 07:08
3

Alternatively, you may perform a certain transformation on the sandwich to get a circle before attempting to use this algorithm. – bright-star Jan 14 '14 at 07:20
1

+1 for introducing the Pizza theorem to me, something I always thought to be true but had never completely worked out. – SQB Jan 14 '14 at 07:30
1

You can subdivide the (square) sandwich in an infinite number of circles, on which you can apply this theorem. Though, lunch time might be over by then.. – Jochem Kuijpers Jan 14 '14 at 12:39
1

It's a cool idea, but ultimately doesn't solve the sandwich-dividing problem, because you can't guarantee straight cuts and you can't guarantee precise angles. Slightly rotate the vertical cut clockwise, and green gets ripped off to black's benefit. – egbrad Jan 14 '14 at 21:41
Is it possible to permute the colors so that any angle deviation penalizes both other players? That would be a start. – bright-star Jan 14 '14 at 21:45
1

I don't think so, because each cut affects four pieces, and there are only three players. Plus, you still cannot guarantee equal divisions, which is really the original problem. I was playing with the following example that exaggerates the "unfair cuts" problem. It would be impossible to distribute the pieces of this "sandwich" fairly, no matter how many players there are: http://i.imgur.com/3H1LWqG.png – egbrad Jan 14 '14 at 21:54

score 14 · Answer 14 · answered Jan 14 '14 at 11:09

The "one person cuts, the other chooses" algorithm generalises to any number of people, but the generalisation is (a) not envy-free; (b) vulnerable to collusion in a subset of at least two of the participants. It does work for cases where one or more participants want a piece of size $ < \frac{1}{n}$, but it splits their share unfairly among the remaining participants.

The participants sit in a circle. Person 0 cuts a portion from the cake. (They don't cut the cake all the way through, but just cut one slice from it.) The resulting portion is offered to person 1. If he accepts it, he takes it and is removed from the circle; otherwise, it's offered to person 2, and so on around the circle. If no one takes it, the portion is returned to person 0, who must take it and is removed from the circle.

This procedure is repeated with the remaining participants (starting with person 1 if they're still present, otherwise person 2), until there is only one person left. This person gets the left-over slice of cake which has never been offered to anyone.

It's clearly very gameable, but if the participants are basically honest, it works well. At least it runs in bounded time and delivers connected portions. Its main practical problem is that one participant can cut a slice that's much too large, advantaging one participant at the expense of all the others. But unlike the "one person cuts all slices" method, the resentment gets to be spread among all the participants who slice, not just focused on one person.

Collusion, though possible, would not be subgame perfect. There are N people. I cut the sandwich into a large piece and N-1 tiny pieces, thinking that the recipient of the large piece will tip me a portion > (1/N). Problem is, they now have their meal, and they don't have to share. Such a bargain could only be enforced because (a) I have a knife, or (b) there is a repeated context, or (c) some other enforcement mechanism outside the game — Paul, Jan 14 '14 at 11:13
That's true, but realistically, context outside the game is likely. Sitting a husband far from his wife would be an obvious precaution, for instance. — Dan Hulme, Jan 14 '14 at 11:22
I think it's just too complex. If player 1 doesn't accept the first portion, and player 2 does, there is something wrong, unless you count other factors (getting a smaller portion instead of waiting longer). — G B, Jan 14 '14 at 12:30
@GB - *"If player 1 doesn't accept the first portion..."* the piece may be a "fair" sized piece (1/n) and so player 2 accepts it. Player 1 may just be waiting for a piece that is larger or smaller (than 1/n), or a piece with a cherry (decoration) on it, or more/less frosting, or just one that "looks" better. — Kevin Fegan, Jan 16 '14 at 20:50
@KevinFegan There goes the "not feeling deceived" part. If different pieces have different (subjective) values, there is no solution. — G B, Jan 17 '14 at 09:14

Kevin Fegan · Answer 15 · 2014-01-15T05:44:05.457

Here's my solution...

Let's say it's a pizza and there are 3 people, but it would work for other items or numbers of people.

The pizza is divided into 3 pieces. It's assumed that the pieces are cut into equal sizes, but it's not important... because the "value" of a piece may not be solely dependent on it's size. For example, a smaller piece may have more of a particular topping, or it may be more/less burned, or thicker/thinner, etc.

Each person identifies the piece they want. If each piece is chosen, then everyone is happy... we're done.

Otherwise, each person "bids" an amount of money they are willing to pay for the piece they want. The piece with the highest bid is set aside for that person.

Bidding continues for the remaining pieces until the last piece (and 1 person) is left.

Everyone pays the amount that they bid, and the last person pays an amount that is the average of all the bids, less the amount that the highest bid exceeded the average (which could be $0 or even less, but that should not be typical).

From this money, the pizza is paid for, and the remaining money is divided equally among all the people.

In the case where the money collected is not enough to pay for the pizza, then everyone pays an equal amount to cover the shortage. Also in this case, you should consider 1: choose another place for your pizza, 2: choose different people to share pizza with.

score 12 · Answer 16 · answered Jan 14 '14 at 12:26

12

Call the players A, B, C:

A cuts the sandwich in two pieces, and calls it "one third" and "two thirds". B can either

accept the "one third" or
choose to cut the "two thirds" in two halves.

In the first case, C gets to cut the "two thirds", and A will choose one of the two halves.

In the second case, C chooses one of the two halves, B gets the other half, and A gets the "one third" he cut at the beginning.

I think it's the easiest possible solution, assuming the players are honest.

answered Jan 14 '14 at 12:26

G B

319

2

Sounds like C loses if A cuts poorly. – gerrit Jan 14 '14 at 12:35
Actually, C has to wait for A and for B to cut/choose, but A "loses" just as much as C. – G B Jan 14 '14 at 12:51
1

This isn't a solution. It only works if the participants are in agreement over the value of each piece. – jwg Jan 14 '14 at 13:13
If each piece has a different value for every player, and the value is unknown to the other players, then there is no solution at all (not even for the simple case of 2 players). – G B Jan 14 '14 at 16:42
1

@GB There are solutions in that case - that's what "envy-free" means. In the case of 2 players, for instance, the person who cut gets what he thinks is an equal share, while the person who chose gets what he thinks is the bigger share. No one feels cheated. – Brilliand Jan 15 '14 at 00:16
1

@GB: The problem is that this is not coalition-resistant. If A and B are friends, then A can cut the sandwich into two equal pieces, so B gets a ½ piece and C is limited to a ¼ piece. Then A and B can get together later and share ¾ of the sandwich. Worse, what if A cuts the sandwich into a huge piece and a tiny piece (e.g., 90% and 10%) and then points to the huge piece and says, “That’s the ⅓ piece.” What recourse does C have then? – Scott - Слава Україні Jan 15 '14 at 01:20
"easiest possible solution, assuming the players are honest". If not, then there is no solution. – G B Jan 15 '14 at 09:27

score 12 · Answer 17 · answered Jan 15 '14 at 22:02

12

I think I have a more practical solution than the one selected:

A cuts the cake in three.
B cuts each piece in three.
C cuts each piece in three.

We now have 27 pieces, each takes one piece in the same order they have cut the cake then reverse the sequence: ABC-CBA-ABC-CBA-...

No matter how A and B cut the cake, C can make sure that every piece is very close to the same size AND it is his best interest to do so. Similarly B, by cutting each piece properly in 3 equal parts, minimizes C's ability to screw up.

A has least incentive to cut fairly, but his cuts have the least influence on the final outcome. He can however set a baseline: if his cuts are fair, no screw-up can be bigger than one third of the cake.

Splitting demo

The assumption here is that none of them is capable of making perfect cuts, but that the errors will cancel themselves out. The important issue is to make it in their best interest to attempt the fairest cuts possible.

By reverting the picking order on each turn, A & C will alternatively chose the biggest remaining piece and B will get the medium piece of each set, so even if there is a discrepancy in the portion sizes the picking order should minimize its impact.

There is also another aspect which is that the greater the number of portions of somewhat similar size, the harder it becomes for each person to keep track of the total amount of cake gotten. With 1 piece each, it's fairly easy for each one to compare portions. But if each person must chose 9 pieces, it's a lot harder to compare the total volume gotten by each.

answered Jan 15 '14 at 22:02

Sylver

1,512

A likes cake and B doesn't like cake, and A and B dislike C, so A cuts one huge and two small pieces, and B cuts each piece into one large and two tiny pieces. A goes first and takes the single huge piece, and B discards whatever crumbs he gets, but this eventually leaves C very sad and hungry. – user21820 Jan 17 '14 at 09:37
Read again and that time do try to understand the solution. A and B cuts the cake into a large one and 2 tiny pieces. Now we have 2 big pieces and a bunch of crumbs. What you didn't understand is that C cuts EACH piece in 3 EQUAL pieces. Nothing A and B can do about it. After C, you have 6 equal pieces and a bunch of crumbs. If C cuts properly, he will get exactly 1 third of the cake. – Sylver Jan 18 '14 at 02:57
I think I responded to the wrong answer, but your method is still wrong. A likes cake and C doesn't like cake, and A and C dislike B, so A cuts equally. If B cuts equally, C cuts all equally except one which he cuts into one large and two tiny, so A goes first and takes that large piece, and B cannot get his fair share. If B does not cut equally, then C cuts equally and I am pretty certain that B also will not get his fair share if both A and C play perfectly. – user21820 Jan 18 '14 at 04:52
You are outside the scope of the question: the original problem was sharing a cake betwen 2 people who want their fair share but don't trust the other. Expanding it to 3 people, we have 3 people who want their fair share. The failure can only occur if C does not actually wants his fair share, in which case most answers above fail completely, whereas my solution limits the failure to a single 1/9th piece. B gets less, but only if C agrees to take even less than B, which is outside the scope of the question asked. – Sylver Jan 18 '14 at 22:20
Ah you interpret the problem differently. The problem never explicitly stated that each of them wants his fair share. It only says that they don't trust each other, and implies that we are to find a procedure by which any player can obtain at least his fair share by playing correctly. But if you assume that every player wants his fair share, then it is enough to let one cut into 3 pieces and the rest choose, since the one cutting will then cut evenly. And I have indeed responded to many answers that fail, not just yours. – user21820 Jan 23 '14 at 01:33
Cutting in 3 one time does not work, because the issue is that they don't trust each other. It is in the first guy's best interest to cut properly, but if he is a lousy cutter there is no mechanism by which the others can correct it. There is also a clear advantage in being able to chose first. If A cuts, which of B or C will chose first? Why? And if A isn't good at cutting, he will get less which is unfair. My solution is not perfect but it gives all players a similar amount of control and avoid creating useless crumbs (cf sol 1). – Sylver Jan 23 '14 at 04:53
Your first objection is invalid because if they don't trust each other then why should you assume that C will play for his own self? B can say that he doesn't trust C to play to benefit himself just as he doesn't trust C to play fairly. Your second objection is also invalid because if A isn't good at cutting, why should you assume that C is? If C isn't, then B can easily get less than his fair share. Your third objection is invalid for a really simple reason. Try cutting a small cake into 27 pieces yourself! Most cakes get deformed or smeared on the plate or stuck on the knife or ... – user21820 Jan 23 '14 at 14:59
That is why we stick to the mathematical form of the game, which has precise strict requirements, as the Wikipedia articles state in detail. Otherwise there is no end to arguing because there is no end to the number of 'real-cake' problems with any cutting procedure whatsoever. – user21820 Jan 23 '14 at 15:01

score 12 · Answer 18 · answered Jan 16 '14 at 22:34

I think I might have an algorithm that a) Is fair b) Can be generalized for n players c) Only uses a bounded number of cuts (a different bound for each n)

odds are that I am wrong =P

The procedure for 3 players:

P1 divides the cake in 3 parts
P2 and P3 choose each a 'smallest piece', such that they dont want part of it.

2.1 If P2 and P3 agree,then they take the 2 pieces they like, and divide each amongst themselves. P3 gets the remaining

2.2 If P2 and P3 disagree, we have: P2 'likes' two pieces P3 'likes' two pieces P1 will be assumed to like the two pieces that are not liked by both P2 and P3 Now, each piece has 2 people that like it. These 2 divide the piece amongst themselves

P1 is happy (if he divided correctly): he either got 1 piece, or half of 2 pieces

P2 and P3 are happy: they each got half of the two pieces they think are bigger

The procedure for n (using the procedure for n-1)

P1 divides in N
Each P2, ..., PN chooses a piece they dislike (and therefore, n-1 they like). They get a 'stake' in each piece they like.
P1 gets 'stakes' in pieces such that each piece is 'divided' in n-1 stakes
recurse: each piece is divided amonsgt the people with stakes on them. If P1 has more then 1 stake, he can 'play as many players' in the division. As far as I can tell, that is not a problem

Yeah, apealing novelty is "don't like" method. I like it. :) — VividD, Jan 16 '14 at 22:45

score 11 · Answer 19 · answered Jan 14 '14 at 13:50

11

It's simple: one person divides the sandwich into 3 pieces, and that person is the last one to choose (the other two can decide using odds and evens, for instance). The dividing person will not want to make no piece larger than another, because he/she would obviously be left with the smaller one.

answered Jan 14 '14 at 13:50

Rodrigo

400

If the first person makes one large piece and two small ones, then the person who picks the large piece will be envied by the person who picks the smaller. – Dan Hulme Jan 14 '14 at 14:19
But why would that person do a large piece, if he/she wouldn't have the chance to eat it? He/she would try the hardest to make the 3 the same size. – Rodrigo Jan 14 '14 at 14:21
1

By accident. Cutting three equal pieces of something is not that easy. – Dan Hulme Jan 14 '14 at 14:26
1

The accident could happen cutting in two, too, even being an easier division. Anyway, @VividD asked for a "such mechanism", not for a "better one". – Rodrigo Jan 14 '14 at 14:31
1

The point is that when cutting in two, only the cutter loses out if they screw up. In your algorithm, the cutter and one other person lose out, so that other person will "feel deceived". – Dan Hulme Jan 14 '14 at 14:39
1

Yes, you're right. But considering the practicality of it, I still recommend my solution. Have you memorized the "Selfridge–Conway discrete procedure" to apply it in the real world in a moment of hunger? :) – Rodrigo Jan 14 '14 at 15:11
the point in the question is that the people don't trust each other. so the first trying "is hardest", dose not make any good in the eye of the 2 others. from their point of view, the pieces could be 0.1, 0.1, 0.8. – user160823 Jul 07 '16 at 18:48
I completely didn't understand your point. – Rodrigo Jul 07 '16 at 23:02
the point is that in your answer, the 3'th person trusts the first rationality(he will want to cut equally),and his percition(he can cut equally), unlike all other answers. the first also trusts that the 2 others, can evaluate "correctly" the 3 pieces, otherwise he could cut in some complicated way, in which the biigets piece looks small. in this case' there is no problem in the first case. – user160823 Aug 12 '16 at 03:16
@user160823 I think you are overcomplicating what is very simple. And you also have a problem with writing correctly. – Rodrigo Aug 12 '16 at 17:12
@Rodrigo in Latex-English, maybe i have. look at some of the other answers, and see that they have the property that no one needs to trust anyone. – user160823 Aug 13 '16 at 19:39
@user160823 In my answer, nobody needs to trust anyone. Maybe (probably) you just didn't understand it. – Rodrigo Aug 14 '16 at 08:57
as good as 1's motivation is, he may cut as follows (maybe he is half blind): 0.1, 0.1, 0.8. then 2 picks the 0.8, and 3 is left without a small piece. what's the probability i did not understand, in your opinion? :) – user160823 Aug 14 '16 at 09:32
The question don't mention blind people. 2. If the first person is blind, how many of the present answers still apply? 3. What if they're all blind? 4. "3 is left WITH a small piece", you mean? As I said, you need to A) read better or B) write better.

Rodrigo

Aug 14 '16 at 09:37

score 10 · Answer 20 · answered Jan 14 '14 at 10:34

It might help what is in the sandwitch. If it's a BLT for example then one of the people might be a vegetarian, but might feel cheated if the other gets more tomato. On the otherhand the bacon will be up for grabs. The lettuce is a wild card of course if they all want it.

I think what you have to do is negotiate sandwitch parts with the others. Perhaps one person will be happy letting the other eat all the bacon if they can eat all the tomato and lettuce. Perhaps one is gluten intolerant so they don't mind the 3rd person having all the bread. The other alternative is for each person to bring their own sandwitches. We had a similar problem like this at work once with pizza and we basically decided not to eat shared pizza anymore.

We had a similar problem like this at work once with pizza and we basically decided not to eat shared pizza anymore. — You must not be mathematicians at work. — gerrit, Jan 14 '14 at 12:32

score 10 · Answer 21 · answered Jan 14 '14 at 21:36

10

Person 1 cut out a 1/3 piece.

Person 2 and 3 decide what piece they want.

If they pick different pieces, the 1/3 piece is given, and other play the 2 people game with the 2/3 piece and players 1.

If they both pick the 2/3 piece, player 1 receives the 1/3 piece and they play the 2 people game with the 2/3 piece.

If they both pick the 1/3 piece, person 2 cut off a part of the 1/3 piece, that part is then added to the 2/3 piece. Person 3 decide if he takes the remaining 1/3 piece, or plays the 2 people game with player 1.

If you do not want to cut the sandwich in more than 3 pieces, go as follow:

Person 1 cut out his piece (1/3);

Person 2 cut out his piece (1/3);

Person 3 can now switch with person 1 or 2 or keep the remaining piece himself.

answered Jan 14 '14 at 21:36

Dorus

381

1

Your first solution is equivalent to the (not envy-free) proportional division given on Wikipedia. Your second solution is incorrect. Person 1 does not like cake and Person 3 likes cake and Persons 1,3 dislike Person 2, so Person 1 cuts a huge piece out and Person 3 will definitely take it, leaving Person 2 forlorn. – user21820 Jan 17 '14 at 10:33
The second solution is obvious less work and therefore less fair; however if you add the assumption that when person 1 cut out 5/6 cake, person 2 and 3 might argue he meant to take only 1/6 part himself. Even when person 1 and 3 work together, this method still makes it hard to give person 2 less than 1/4th of the cake. If person 2 expect treason, person 1 can give him 1/2 cake and he can cut it into 1/4th parts. It works of course better when all players try to maximize there share. – Dorus Jan 20 '14 at 14:57
Also i did not read wikipedia but nobody else here mentioned that specific way so i tought it was fair to add it. – Dorus Jan 20 '14 at 14:59
I can understand, but we would like to have correct solutions listed here, so if there are like twenty solutions every reader will have to take a long time to think through every single solution, and in that case I would rather go to Wikipedia than come here to find the answer to this question. That said, I commented only to demonstrate that it is not as easy as one might think at first glance, and if you try to prove any of the correct solutions you will find that it is even harder to prove than to devise them. – user21820 Jan 23 '14 at 01:23
Also, if players always maximize their share, then it suffices to have one player cut the cake into 3 pieces and the rest choose one for each of themselves. – user21820 Jan 23 '14 at 01:24
@user21820 Ah thanks, your last comment made sense, i understand the problem now. Learning something new every day :) As for the wikipedia argument: Over half the questions and answers on stackexchange could probably be referred to wikipedia, so that point is mood. – Dorus Jan 23 '14 at 19:26

score 10 · Answer 22 · answered Jan 15 '14 at 09:37

10

Take the sandwich and divide it into 4 even squares, take 1 of the squares and cut it evenly into 3 rectangular pieces. Everyone now gets a big square and a small rectangular piece.

answered Jan 15 '14 at 09:37

Benjamin

117

This solution is vaguely reminiscent of Egyptian fractions and becomes very appropriate if you wanted to divide two sandwiches between three people (each gets 2/3). The Egyptian fraction for 2/3 is: 1/2 + 1/6. Thus, you would divide the sandwich into halves and the remaining half into sixths. (See the "practical use of Egyptian fractions" in the link). – Jan 26 '14 at 23:23

score 8 · Answer 23 · answered Jan 14 '14 at 14:49

8

This may be silly, but I think it's fairly straightforward for as many people as you want. If you have $n$ people, order person number $1$ to cut the sandwich into $n$ pieces. All the other $n-1$ people then pick their own piece. The person who was cutting gets the piece that was left. If he cut all pieces equally, he will have $1/n$ of the sandwich. If any one piece was bigger, this means one piece had to be smaller, and the smaller piece will not get selected, so the cutter has motivation to cut equally.

answered Jan 14 '14 at 14:49

5xum

126,227
6
135
211

3

What if... Person number 1 doesn't really care that much if their piece is a little smaller and that lack of care is reflected in their cutting accuracy. So person 2 selects the biggest piece and person 3-n are left to choose from smaller pieces, leaving the smallest piece for person 1. The only person happy with this is person 2 (and perhaps person 1 who didn't care). The others are left to wonder why person 2 was able to choose first. Even if person 1 cut carefully, some may view person 2's ability to choose first as being unfair. – Kevin Fegan Jan 14 '14 at 20:14
This comment can also be applied to the original case, so I don't think it's all that relevant. I think the task only makes sense if all the people present have the same measure of fairness and are equally interested in it. With those assumptions, my method works. – 5xum Jan 14 '14 at 20:52
1

It is different. In the original case, with 2 people, if the cutter didn't care and cut poorly (for any reason), the chooser would be happy, and the cutter would be happy (didn't care). The same is the case for the first-chooser and the cutter with 3 or more people (or if the cutter can't cut accurately). The difference is, the remaining "middle" people have no control of the outcome if they are not happy with their piece, compared to pieces choosen before they were able to choose. – Kevin Fegan Jan 14 '14 at 21:17
Point taken. I admit my method needs slighlty stronger assumptions if there are 3 od more people. I still kinda like it, though. – 5xum Jan 16 '14 at 10:20
It is a "classic" method... it's hard to beat the classics. – Kevin Fegan Jan 16 '14 at 19:54

VividD · Answer 24 · 2015-04-16T18:03:34.120

This presentation contains background and main results in resource allocation and fair division areas. "A cake" is formally defined as (0,1) interval. The author outlines and compares eight procedures for fair division of a cake. For the sake of comparison, following properties of fair division procedures are defined: proportionality, envy-freeness, equability, Paretto-efficiency. Some of the procedures require a referee, and some do not. Some produce contiguous pieces, some do not. All procedures are evaluated against the set of properties above.

Following table from the presentation summarizes features of described procedures:

Regarding avoiding envy, the authors even mention and define degree of envy-freeness for some of presented procedures.

The key conclusion of the presentation is:

The problem becomes non-trivial for more than two players, and there are many open problems relating to finding procedures with “good” properties for larger numbers of players.

score 7 · Answer 25 · answered Jan 14 '14 at 08:12

Hmm, if you cut it into an approximate 3rd and 2/3rds portions, then the cutter would get a slice that both other people think is about 1/3rd. To attempt to subvert this, player A could cheat and make 2 equal halves. In the real world, such a player would never get invited to party games again. ;) But let's just say that then one of the other players would have to divide each half into 1/6th and 1/3rd slices. Repeat ad nauseum?

If you can 'uncut' the sandwich, then it's easier: Just keep having a different player cut the sandwich until the other 2 agree. This is similar to the moving-knife solution but where the cut is not done unless all 3 agree, in actual practice since 'uncutting' really means just not cutting yet.

Once you get the bigger piece being roughly 2/3rds, then you can apply the normal 2-person method. To go to 4 people, vote in pairs? You could also apply this idea with 1/4th & 3/4ths slices. This is generalizable to 5,...,dozens of people.

D.R. · Answer 26 · 2025-01-03T02:00:04.253

The YouTube channel Up and Atom made a video discussing the solution (envy-free division for an arbitrary number $n$ of players!), due to Mackenzie and Aziz "A DISCRETE AND BOUNDED ENVY-FREE CAKE CUTTING PROTOCOL FOR ANY NUMBER OF AGENTS". https://www.youtube.com/watch?v=fvM8ow6zNw4&ab_channel=UpandAtom It's a wonderfully friendly, intuitive explanation of a pretty difficult problem!

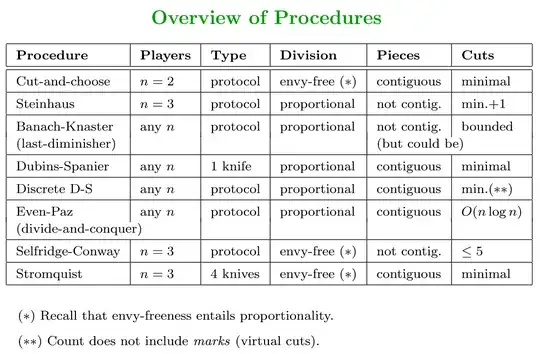
Jade first explains the Selfridge-Conway Protocol (discussed in previous MSE answers --- the overarching structure that is relevant for my answer is that it happens in 2 Phases, Phase 1 divvying up most of the cake, and Phase 2 splitting the remainder/"residue"), introducing the idea of

DEF: a player $P_1$ dominating another player $P_2$: when $P_1$ can give all the residue to $P_2$ without getting envious (of $P_2$).

(in particular, this means $P_1$ is happy to let $P_2$ make choices about the residue piece before $P_1$ makes any choice about the residue piece)

Example: for $n=3$: at some Stage, we have a piece of cake on the table (could be the original cake, or the residue after some preceding Stage).

If $P_1$ ("the initial cutter for this stage") cuts a piece into 3 "main pieces" that $P_1$ thinks are all equal in value, and $P_2$ cuts one of the "main pieces" into 2, one of which we will still call a "main piece" (which we'll also call the "co-residue piece") and one called the "residue piece". (So 4 total pieces, 3 "main", one of which has an extra adjective "coresidue".)

And suppose that we can distribute the 3 "main" pieces to the 3 players so that everyone is envy-free (with what they have so far). Suppose $P_i$ ($i\neq 1$) gets the main-coresidue piece. Then $P_1$ dominates $P_i$, because [main-coresidue + residue] was one of the 3 original "main pieces" $P_1$ considered all equal.

If this doesn't make sense watch the video. Jade explains it much better, with much better visuals!

and the idea that the algorithm should ask any cutter $C$ to cut in a way that they think that some set $\mathscr S$ of the pieces are equal, and hence happy to let other players choose amongst the pieces in $\mathscr S$ before $C$'s own choice.

The key behind the new solution is the insight that if we get to some stage where there's some remainder/residue left on the table, and $P_1$ dominates every other player (i.e. is happy to give all the residue to the other players), then we can remove $P_1$ from consideration, since $P_1$ is happy with what they have and will never get envious of the other players, no matter how we divvy up the residue!

The method for how to get to the point where 1 player dominates the rest is difficult. The key idea is to swap pieces of cake previously already agreed upon/allocated, in a way that keeps people envy-free; and take advantage of the the phenomenon in the Example above that at any Stage, $P_\text{initial cutter for Stage}$ always dominates $P_\text{took co-residue}$, so if we swap around who gets the co-residue, $P_\text{init. cutter}$ can dominate more people. Watch the video or read the paper for more information.

Splitting a sandwich and not feeling deceived

26 Answers26

edit: I'm more confident about this one.

Linked

Related