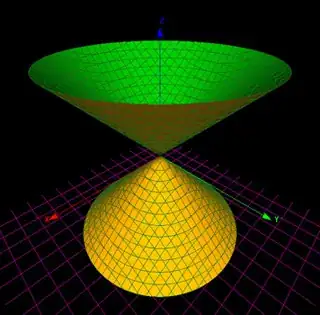
$ X = V(z^2-x^2-y^2)$, known as a cone. (See the picture.) However, for any point $p \in X$ other than $0$ there is only one line going through $p$ and contained in $X$.
Indeed, the plane is the only surface which contains three lines going through each of its points.
In higher dimensions, there are more varieties with this property. (For example, you can consider the product $X \times \mathbb{A}^{2}_{\mathbb{C}}$ for an arbitrary $X$.)
If you want a nonsingular example, consider the surface $X$ defined by $z = xy(x-y)$. You probably can't visualise this, but algebraically it is easy to see that there are three lines on $X$ going through $0$. They are the lines defined by $z = x = 0$, $z = y = 0$ and $z = x-y = 0$.
Let me explain how I came up with this example. First, let us look at the "saddle surface" $S = V(z - xy)$. You have probably already seen $S$ at some point. If not, I hope you can find a good picture online somewhere, or maybe visualise it yourself. The point is, that contained in $S$ we find the $x$-axis and the $y$-axis. The reason is that, when we look at $S$ only in the xy-plane which is defined by $z = 0$ the defining equation reduces to $xy = 0$, which corresponds to the two coordinate axes. Now when we want to have three lines on our surface, we can just start with the equation $xy(x-y) = 0$, which describes the coordinate axes and a diagonal line, and then add a parameter $z$ to get $V(xy(x-y) - z) \subseteq \mathbb{R}^{3}$.
If we push this trick further, we can get an arbitrary number of lines in our surface, and I guess it starts looking like this: