Biggest powers NOT containing all digits.

Question

Let $m>1$ be a natural number with $m \not\equiv 0 \pmod{10}$

Consider the powers $m^n$ , for which there is at least one digit not occurring in the decimal representation.

Is there a largest $n$ with the desired property for any $m$? If so, define $n(m)$ to be this number.

Examples :

$$m=2 \rightarrow 2^{168} = 374144419156711147060143317175368453031918731001856$$

does not contain the digit $2$.

All the powers above up to $2^{10000}$ conatin all the digits, so $2^{168}$ seems to be the biggest power with the desired property.

$$m=3 \rightarrow 3^{106} = 375710212613636260325580163599137907799836383538729$$

does not contain the digit $4$.

All the powers above up to $3^{10000}$ contain all the digits, so $3^{106}$ seems to be the biggest power with the desired property.

So, probably $n(2)=168$ and $n(3)=106$ hold.

Is $n(m)$ defined for any $m$, and if yes, can reasonably sharp bounds be given?

Searching for "168, 106" was enough to find it in OEIS: http://oeis.org/A062518 — Bart Michels, Jan 04 '14 at 21:52
An amazing example is $476^{41}$ with 110 digits containing no 3. — Peter, Jan 04 '14 at 22:15
Even more amazing is $1955^{39}$ with 129 digits conatining no 1. — Peter, Jan 04 '14 at 22:20
But $n$ can be as high as infinite. I imagine it is possible for their to be higher powers than 168 for 2. Think about it this way. $2^x$ has $f(x)$ digits. The odds of any digit being 2 is approximately 1 out of 10. Truthfully, 2 does not appear randomly, but if it did, then... the odds of 2 appearing $g(x)$ times is approximately $f(x)/10$. Or $g(x)\approx f(x)/10$ — Simply Beautiful Art, Dec 18 '15 at 00:50
Another record-breaker: $1274902129^{24}$ has 219 digits and no digit 4. — Oldboy, Dec 25 '18 at 09:20

score 8 · Accepted Answer · edited Jan 01 '25 at 02:27

Some obesrvations:

I have tested $2^n$ up to $n$=250000 and found that $n(2)=168$ still holds. Having played with this problem a lot I conjecture that $n(m)\le168$ for all $m$.

I went a little bit further down the road and found the following values for numbers up to 340. All values have been obtained by calcuating all powers up to power 50000 and getting the biggest power with a digit missing in the result.

I have also checked values $n(m)$ in the range $m=10^6...10^9$ and found local maximums to go down from around 20 to 10. And from time to time you can find a real gem:

$32886598^{26} = \\ 2770082411 \ 7701047414 \ 3812147939 \ 0119763476 \ 3327029432 \\ 3084767371 \ 7070016012 \ 4780829912 \ 9634078101 \ 6224929090 \\ 6339478284 \ 9104901979 \ 0146722638 \ 7896000449 \ 7946341749 \\ 3932606670 \ 3148399037 \ 2721668024 \ 4923962610 \ 417664$

196 digits with digit 5 missing.

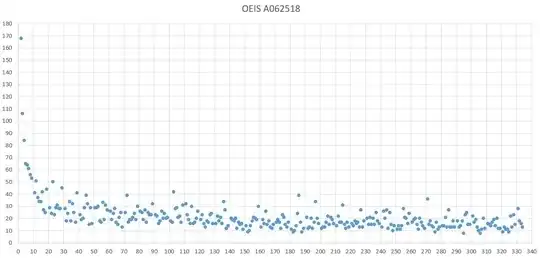
(2,168), (3,106), (4,84), (5,65), (6,64), (7,61), (8,56), (9,53), 
(11,41), (12,51), (13,37), (14,34), (15,34), (16,42), (17,27), (18,25), (19,44), 
(21,29), (22,24), (23,50), (24,23), (25,29), (26,31), (27,), (8), (28,28), (29,45), 
(31,28), (32,18), (33,24), (34,34), (35,18), (36,32), (37,25), (38,17), (39,41), 
(41,23), (42,19), (43,20), (44,29), (45,39), (46,32), (47,15), (48,29), (49,16), 
(51,29), (52,29), (53,30), (54,18), (55,17), (56,33), (57,19), (58,31), (59,27), 
(61,26), (62,19), (63,24), (64,28), (65,17), (66,15), (67,21), (68,25), (69,13), 
(71,25), (72,39), (73,17), (74,19), (75,19), (76,21), (77,24), (78,19), (79,30), 
(81,26), (82,25), (83,19), (84,27), (85,17), (86,25), (87,23), (88,23), (89,32), 
(91,23), (92,22), (93,16), (94,18), (95,26), (96,20), (97,24), (98,20), (99,21), 
(101,18), (102,17), (103,42), (104,28), (105,29), (106,21), (107,22), (108,17), (109,31), 
(111,32), (112,23), (113,19), (114,16), (115,30), (116,16), (117,17), (118,20), (119,26), 
(121,19), (122,23), (123,16), (124,13), (125,18), (126,17), (127,23), (128,24), (129,16), 
(131,16), (132,22), (133,18), (134,21), (135,16), (136,34), (137,27), (138,12), (135,16), (136,34), (137,27), (138,12), (139,14), 
(141,20), (142,19), (143,18), (144,20), (145,12), (146,17), (147,15), (148,16), (149,11), 
(151,14), (152,9), (153,10), (154,14), (155,18), (156,21), (157,20), (158,19), (159,30), 
(161,13), (162,19), (163,16), (164,26), (165,15), (166), (18), (167,13), (168,12), (169,15), 
(171,17), (172,19), (173,17), (174,12), (175,23), (176,21), (177,15), (178,13), (179,17), 
(181,11), (182,9), (183,10), (184,14), (185,24), (186,39), (187,17), (188,9), (189,12), 
(191,21), (192,12), (193,13), (194,20), (195,12), (196,17), (197,34), (198,20), (199,16), 
(201,12), (202,13), (203,13), (204,17), (205,22), (206,15), (207,21), (208,19), (209,16), 
(211,14), (212,22), (213,17), (214,17), (215,31), (216,15), (217,12), (218,17), (219,13), 
(221,16), (222,14), (223,18), (224,16), (225,17), (226,13), (227,27), (228,13), (229,18), 
(231,20), (232,15), (233,21), (234), (15), (235,20), (236,15), (237,25), (238,18), (239,16), 
(241,13), (242,26), (243,20), (244,27), (245,12), (246,25), (247,15), (248,10), (249,14), 
(251,11), (252,14), (253,11), (254,14), (255,28), (256,), (1), (257,20), (258,16), (259,24), 
(261,17), (262,19), (263,20), (264,15), (265,11), (266,20), (267,17), (268,14), (269,12), 
(271,36), (272,15), (273,18), (274,14), (275,13), (276,9), (277,17), (278,11), (279,13), 
(281,14), (282,14), (283,21), (284,13), (285,27), (286,13), (287,13), (288,18), (289,13), 
(291,18), (292,13), (293,14), (294,18), (295,8), (296,23), (297,25), (298,15), (299,15), 
(301,22), (3), (2,17), (303,19), (304,13), (305,10), (306,8), (307,11), (308,20), (309,12), 
(311,16), (312,15), (313,14), (314,17), (315,19), (316,14), (317,20), (318,12), (319,12), 
(321,9), (322,13), (323,11), (324,11), (325,9), (326,22), (327,13), (328,23), (329,15), 
(331,28), (332,18), (333,16), (334,13) ...

If you are interested in the length of the result, a few items from this list will "raise the bar":

$2^{168}$ has 51 digits.

$7^{61}$ has 52 digits.

$12^{51}$ has 56 digits.

$19^{44}$ has 57 digits.

$23^{50}$ has 69 digits.

$72^{39}$ has 73 digits.

$103^{42}$ has 85 digits.

$186^{39}$ has 89 digits.

$349^{39}$ has 100 digits.

$476^{41}$ has 110 digits.

$1955^{39}$ has 129 digits.

$42806^{30}$ has 139 digits.

$165541^{27}$ has 141 digits.

$191131^{27}$ has 143 digits.

$700419^{25}$ has 147 digits

$700419^{25}$ has 147 digits.

$874395^{27}$ has 161 digits.

$4408232^{25}$ has 167 digits.

$5397917^{27}$ has 182 digits.

$8751594^{27}$ has 188 digits.

$32886598^{26}$ has 196 digits

$54013149^{28}$ has 217 digits

$1274902129^{24}$ has 219 digits

$1337169719^{24}$ has 220 digits

EDIT: Current record:

$1419213312^{25}$ has 229 digits and no digit 7

Thank you for the search, +1 especially for the $196$-digit example. — Peter, Dec 16 '18 at 12:15
@Peter I'm still running some code. I don't want to stop now that I'm so close to 200-digit limit. — Oldboy, Dec 16 '18 at 12:29
Also 217 digits: $1000000001^{24}$, without digit 8. And this can be infinitely expanded to $(10^n+1)^{24}$ where $n\ge 7$, because \begin{pmatrix}24\m\end{pmatrix} does not contain a single 8 for all $0\le m\le 24$. — Shieru Asakoto, Jun 16 '25 at 04:45

Adam Scherlis · Answer 2 · 2025-01-03T03:18:09.810

We can give a heuristic argument that $\limsup_m n(m) = 21$. [Edit: this originally said 22 due to a sign error.]

Fix a value of $n$. Consider some $m$. Define $L = \log_{10}(m)$.

$m^n$ has $n L + O(1)$ digits in base ten.

The probability that these take at most 9 distinct values is

$$\left(\frac9{10}\right)^{n L + O(1)} = m^{n \log_{10}(9/10)}\times O(1).$$

Across all values of $m$, the expected number of solutions will be

$$O(1) \times \sum_m m^{n \log_{10}(9/10)}.$$

This diverges iff $n \log_{10}(9/10) \ge -1$, i.e. iff

$$n \le \frac1{1 - \log_{10}9} \approx 21.85$$

So there are "probviously" an infinite number of solutions for $n=21$, and "probviously not" if $n\ge 22$.

This seems consistent with the data above, where the exponents seem to be dropping towards a limit in the low 20's.

(A more intuitive handwavy version of this argument is that this is the size of $n$ at which the number of digits in $m$ balances out against the log-improbability, giving you "enough degrees of freedom" to find a solution.)

It's also not too hard to (less rigorously) estimate $n^\star(m_0) = \sup_{m>m_0} n(m)$, which is roughly what those data are showing, with something along the lines of

$$n^\star \approx \left(1 + \frac{\log n^\star}{\log m}\right)\frac1{1 - \log_{10}9}$$

which is a transcendental equation but easy to compute iteratively. The idea here is that the digits of $n$, in addition to the digits of $m$, provide "degrees of freedom" that balance against the improbability. This seems to be fairly accurate in practice, overestimating a bit for small $m$.

score 0 · Answer 3 · edited Jun 25 '18 at 21:15

0

The bound is improved to $2^{100000}.$ I read it on an OEIS website about Zerofree powers

edited Jun 25 '18 at 21:15

Adrian Keister

10,272

answered Jun 25 '18 at 18:42

OEIS

101

@RossMillikan: Oh, thanks. I was aware of that, but didn't double-check my work. – Adrian Keister Jun 25 '18 at 21:16
An even more amazing example is 6161527^21 with 143 digits containing no 0. – OEIS Jun 27 '18 at 16:38
I just learned a larger one! 92364991^22 with 176 digits containing no 0. – OEIS Jun 27 '18 at 16:56
@JenaroTomaszewski My one beats all :) $32886598^{26}$ has 196 digits with digit 5 missing. Please check my observations below. – Oldboy Dec 16 '18 at 11:58

Biggest powers NOT containing all digits.

3 Answers3

Linked

Related