Mixed equation: sum of $\cos(x)$ term and polynomial in x$

Question

Can you help me with the following equation $$\dfrac{x^2}{2} - \cos x - 1 = 0$$

I cannot find $x.$

Answer 1

$$\dfrac{x^2}{2} - \cos x - 1 = 0 \iff x^2 - 2\cos x - 2 = 0\iff 2\cos x = x^2 - 2$$

This is the type of exercise which may best be approached through graphing the equation. The graph of the equation reveals a parabola-like curve, which is symmetric about the y-axis, and which has two real roots (two solutions), the exact values of which we can approximate:

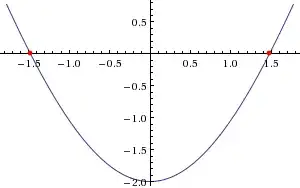
$\quad x \approx -1.478, \qquad \qquad \qquad x \approx 1.478$.

Answer 2

Lets clean up the equation a bit and see if that leads anywhere.

Firstly use the following trigonometric identity:

$$\cos 2u = 2 \cos^2 u - 1$$

Substituting leaves only squared terms:

$$\frac{x^2}{2} - 2 \cos^2 \frac{x}{2} = 0$$

$$\left(\frac{x}{2}\right)^2 = \cos^2 \frac{x}{2}\iff \frac{x}{2} = \pm \cos\frac{x}{2}$$

The solution to $\cos \theta = \theta$ is $\theta \approx 0.739085$ (see this question) so your solution is $x\approx\pm 1.47817$.

Answer 3

This class of equations cannot be solved analytically but only using a numerical method. For sure, as suggested by amWhy, graphing the equation is avery good practice which allows to see the shape of the function and to locate more or less accurately where are the roots.

If you want to polish the root (basically to any accuracy you could desire), Newton method is very good—provided that you have a "reasonable" guess of the root you are looking for.

For your specific problem, say that the root is close to $1.5$; we shall name it $x_\text{old}$. Now, Newton iterations make the update according to the following scheme: $$x_\text{new} = x_\text{old} - \frac{f(x_\text{old})}{f'(x_\text{old})}.$$

This produces the following iterates: $1.47827, 1.47817, \dotsc$.