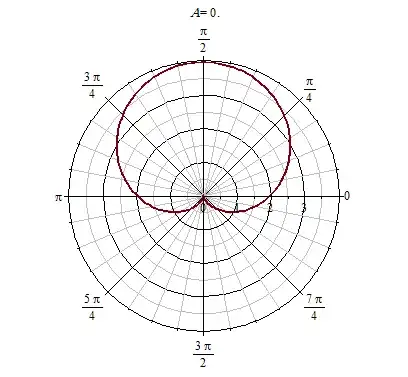
How can an equation for the following curve be derived?
$$r=(1+0.9 \cos(8 \theta)) (1+0.1 \cos(24 \theta)) (0.9+0.1 \cos(200 \theta)) (1+\sin(\theta))$$
(From WolframAlpha)
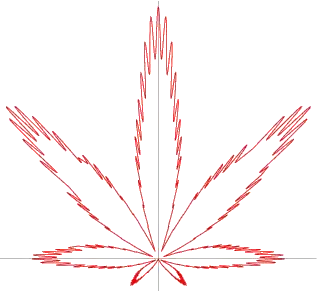
How can an equation for the following curve be derived?

$$r=(1+0.9 \cos(8 \theta)) (1+0.1 \cos(24 \theta)) (0.9+0.1 \cos(200 \theta)) (1+\sin(\theta))$$
(From WolframAlpha)
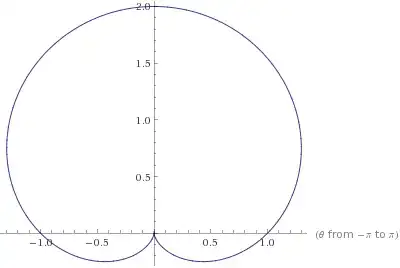
It can be made intuitively out of the following observations:

Finally, all of this points to this
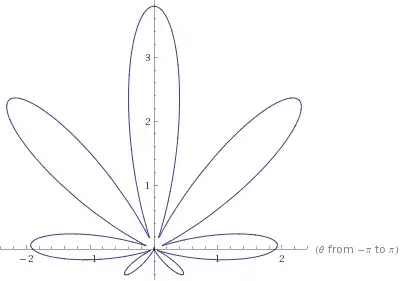
The remaining factors, which have much smaller periods, and expand/contract the radio much less, are there just to make the "borders" looks less regular.
You may do the same as other answer did in details by Maple:
[> with(plots):
animate(polarplot, [(1+.9*cos(A*t))*(1+.1*cos(A*t))*(.9+0.5e-1*cos(A*t))*(1+sin(t)), t = -Pi .. Pi, thickness = 2], A = 0 .. 15);