I) OP considers the TISE
$$ \hbar^2\psi^{\prime\prime}(x) +\alpha (x\!-\!x_0)\psi(x)~=~0, \qquad \alpha~\neq~0,\tag{1}$$
with an affine potential, i.e. the Airy differential equation (DE). We need to find 2 independent solutions. Here $\alpha\in \mathbb{R}\backslash\{0\}$ is a non-zero real constant, and $x_0$ is a turning point, i.e. the boundary point between the classically allowed and forbidden $x$-regions.
II) OP's idea is good. If we Fourier transform
$$\tilde{\psi}(p)
~=~ \int_{\mathbb{R}} \! \frac{\mathrm{d}x}{\sqrt{2\pi \hbar}}~\exp\left( -\frac{ipx}{\hbar} \right) \psi(x) \tag{2}$$
the source-free/homogeneous second-order ODE (1), we get a source-free/homogeneous first-order ODE
$$ i\hbar\tilde{\psi}^{\prime}(p) - \left(x_0+\frac{p^2}{\alpha}\right)\tilde{\psi}(p)~=~ 0,\tag{3} $$
with solution
$$ \tilde{\psi}(p)~=~\exp\left( -\frac{i}{\hbar} \tilde{S}(p)\right),\qquad \tilde{S}(p)~:=~p\left(x_0+\frac{p^2}{3\alpha}\right),\tag{4} $$
up to an overall normalization factor.
III) Eqs. (2) and (4) suggest that we should consider the contour integral
$$ \psi(x)~=~\int_{\gamma} \! \frac{\mathrm{d}p}{\sqrt{2\pi \hbar}}~\exp\left(\frac{i}{\hbar} \left(px-\tilde{S}(p)\right)\right), \tag{5} $$
where $\gamma$ is an open contour between exponentially suppressed sectors $|p| \to \infty$ in the complex $p$-plane, such that the integral (5) is well-defined and convergent.
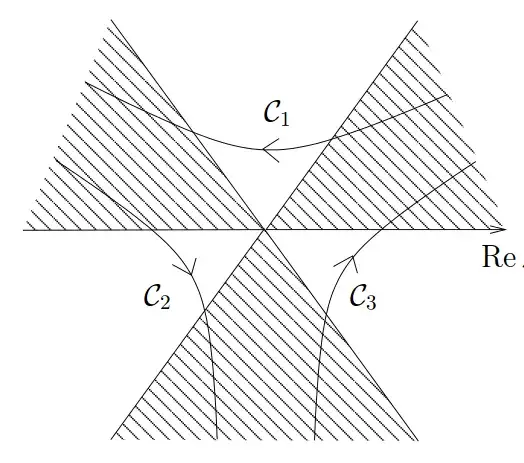
$\uparrow$ Fig. 1. The complex $p$-plane with 3 possible integration contours ${\cal C}_1$, ${\cal C}_2$, ${\cal C}_3$ in the case $\alpha<0$. The shaded regions denote exponentially decaying sectors. The Airy function ${\rm Ai}$ has the opposite integration contour of ${\cal C}_1$, while ${\rm Ci}$ has integration contour ${\cal C}_3$. (Figure taken from Ref. [W].)
IV) The contour integral (5) indeed satisfies the Airy DE (1):
$$\begin{align} \hbar^2\psi^{\prime\prime}(x) +\alpha (x\!-\!x_0)\psi(x)
~\stackrel{(5)}{=}~&\int_{\gamma} \! \frac{\mathrm{d}p}{\sqrt{2\pi \hbar}}~\left(-p^2 +\alpha (x\!-\!x_0)\right)
\exp\left(\frac{i}{\hbar} \left(px-\tilde{S}(p)\right)\right)\cr
~=~&-i\hbar\alpha \int_{\gamma} \!\frac{\mathrm{d}p}{\sqrt{2\pi \hbar}}~\frac{d}{dp}\exp\left(\frac{i}{\hbar} \left(px-\tilde{S}(p)\right)\right)~=~0.\tag{6}\end{align} $$
Since the integrand (5) is an entire function in $p$, the $p$-integral (5) only depend on the monodromy of the contour. Since there are 3 exponentially decaying sectors, there are 2 independent contours, leading to 2 independent solutions (5) to the Airy DE (1). Particular choices of the contour $\gamma$ lead to integral representations for the Airy functions ${\rm Ai}$ and ${\rm Bi}$ up to affine scaling.
V) To illustrate the powerful integral representations of ${\rm Ai}$ and ${\rm Bi}$ let us for the remainder of this answer for fun work out the corresponding WKB connection formulas.
The Airy functions ${\rm Ai}$ and ${\rm Bi}$ are defined as follows:
$$ {\rm Ai}(x)~:=~ \int_{\mathbb{R}_+}\frac{\mathrm{d}k}{\pi} \cos \left(\frac{k^{3}}{3}+ xk\right)
~=~ \int_{\mathbb{R}+i0^+}\frac{\mathrm{d}k}{2\pi} e^{i S(k,x)} ,\tag{7} $$
$$ {\rm Bi}(x)~:=~{\rm Bi}_e(x) + {\rm Bi}_s(x)
~\stackrel{(9)+(10)+(11)}{=}~{\rm Ci}(x)+i{\rm Ai}(x), \tag{8}$$
$${\rm Bi}_e(x)~:=~ \int_{\mathbb{R}_+}\frac{\mathrm{d}\kappa}{\pi} \exp \left(-\frac{\kappa^{3}}{3} + x\kappa\right)
~\stackrel{\kappa=ik}{=}~\int_{-i\infty}^{0}\frac{\mathrm{d}k}{\pi i} e^{i S(k,x)} , \tag{9}$$
$$\begin{align} {\rm Bi}_s(x)~:=~& \int_{\mathbb{R}_+}\frac{\mathrm{d}k}{\pi} \sin \left(\frac{k^{3}}{3} + xk\right)
~=~ \int_{\mathbb{R}+i0^+}\frac{\mathrm{d}k}{2\pi i} {\rm sgn}(k) e^{i S(k,x)} \cr
~=~& \int_{\mathbb{R_+}+i0^+}\frac{\mathrm{d}k}{\pi i} e^{i S(k,x)} + i{\rm Ai}(x), \end{align}\tag{10}$$
$${\rm Ci}(x)~:=~\left( \int_{-i\infty}^{0}+ \int_{\mathbb{R_+}+i0^+}\right) \frac{\mathrm{d}k}{\pi i} e^{i S(k,x)} , \tag{11}$$
$$ S(k,x) ~:=~kx + \frac{k^3}{3}, \quad S^{\prime}(k,x) ~=~x + k^2, \quad S^{\prime\prime}(k,x) ~=~2 k. \tag{12} $$
Note that the contour for the ${\rm Ci}$ function goes along the boundary of the fourth quadrant in the complex $k$-plane, cf. Fig. 1.
VI) We next use the method of steepest descent
$$\begin{align} \int_{\gamma} \mathrm{d}k~ e^{i S(k,x)}
~=~&\sqrt{|x|} \int_{\gamma/\sqrt{|x|}}\mathrm{d}k~ e^{i|x|^{3/2} S(k,{\rm sgn}(x))} \cr
~\sim~&\sum_{\pm} \sqrt{\frac{2\pi i}{S^{\prime\prime}(k_{\pm},x)}} e^{i S(k_{\pm},x)} \quad {\rm for}\quad |x|\to \infty.\end{align} \tag{13} $$
There are 2 stationary points $k_{\pm}$.
VII) Case $x>0$:
$$k_{\pm} ~=~ \pm i \sqrt{x}, \qquad S(k_{\pm},x) ~=~\pm i \frac{2}{3}x^{3/2}.\tag{14}$$
Line of steepest descent: Upper sign: Horizontal. Lower sign: Vertical.
This leads to the following asymptotic formulas:
$$\begin{align} {\rm Ai}(x)~\stackrel{(7)+(13)}{\sim}&\frac{1}{2\sqrt{\pi}x^{1/4}}\exp\left(-\frac{2}{3}x^{3/2}\right),\tag{15}\cr
{\rm Ci}(x)~\stackrel{(11)+(13)}{\sim}&\frac{1}{\sqrt{\pi}x^{1/4}}\exp\left(\frac{2}{3}x^{3/2}\right)
+ \frac{1}{2i\sqrt{\pi}x^{1/4}}\exp\left(-\frac{2}{3}x^{3/2}\right), \tag{16}\cr
{\rm Bi}(x)~\stackrel{(8)}{=}~&{\rm Ci}(x)+i{\rm Ai}(x)
~\stackrel{(15)+(16)}{\sim}~
\frac{1}{\sqrt{\pi}x^{1/4}}\exp\left(\frac{2}{3}x^{3/2}\right), \tag{17}\end{align} $$
for $x\to \infty$. In eq. (16) we counted the exponentially subdominant contribution from the stationary point $k_+$ with a weight $\frac{1}{2}$ since we only integrate $\frac{1}{2}$ of the Gaussian. In eqs. (15) resp. (17) we excluded the purely imaginary contributions from the dominant $k_-$ resp. subdominant $k_+$, partly because the ${\rm Ai}$ and ${\rm Bi}$ functions are manifestly real. In this way we use the reality structure to make the WKB connection formulas 2-ways.
VIII) Case $x<0$:
$$k_{\pm} ~=~ \pm \sqrt{-x}, \qquad S(k_{\pm},x) ~=~\mp \frac{2}{3}(-x)^{3/2}.\tag{18}$$
Line of steepest descent: $\pm \frac{\pi}{4}$.
This leads to the following asymptotic formulas:
$$\begin{align} {\rm Ai}(x)~\stackrel{(7)+(13)}{\sim}&\frac{1}{2\sqrt{\pi}(-x)^{1/4}}\sum_{\pm} \exp\left(\pm i\left(\frac{\pi}{4}-\frac{2}{3}(-x)^{3/2}\right)\right)\cr
~=~&\frac{1}{\sqrt{\pi}(-x)^{1/4}} \cos\left(\frac{2}{3}(-x)^{3/2}-\frac{\pi}{4}\right)\cr
~=~&\frac{1}{\sqrt{\pi}(-x)^{1/4}} \sin\left(\frac{2}{3}(-x)^{3/2}+\frac{\pi}{4}\right),\tag{19}\cr
{\rm Ci}(x)~\stackrel{(11)+(13)}{\sim}& \frac{1}{i\sqrt{\pi}(-x)^{1/4}} \exp\left( i\left(\frac{\pi}{4}-\frac{2}{3}(-x)^{3/2}\right)\right)\cr
~=~&\frac{1}{\sqrt{\pi}(-x)^{1/4}} \exp\left(- i\left(\frac{2}{3}(-x)^{3/2}+\frac{\pi}{4}\right)\right)
,\tag{20} \cr
{\rm Bi}(x)~\stackrel{(8)}{=}~&{\rm Ci}(x)+i{\rm Ai}(x)
~\stackrel{(19)+(20)}{\sim}~
\frac{1}{\sqrt{\pi}(-x)^{1/4}} \cos\left(\frac{2}{3}(-x)^{3/2}+\frac{\pi}{4}\right),\tag{21} \end{align}$$
for $x\to -\infty$.
References:
- [W] E. Witten, Analytic Continuation Of Chern-Simons Theory, arXiv:1001.2933; p. 23-29, 48-49. A related 2015 KITP lecture by Witten, A New Look At The Path Integral Of Quantum Mechanics, can be found on YouTube.
