1

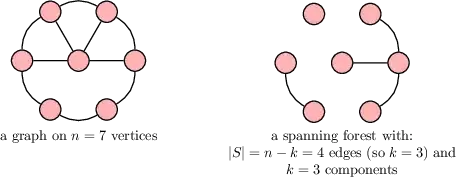
The following proposition about the number of components in a spanning forest of a graph $G$ has an easy inductive proof. You are asked to provide it in the exercises.

Proposition 12.1. Let $G=(V,E)$ be a graph on $n$ vertices, and let $H=(V,S)$ be a spanning forest. Then $0 \leq |S| \leq n-1$. Furthermore, if $|S|=n-k$, then $H$ has $k$ components. In particular, $H$ is a spanning tree if and only if it contains $n-1$ edges.

I am studying Graph Algorithms. I can solve the graph algorithm problems but I am confused with this proposition. If I were to prove this proposition, how would I start? Can anyone help here? Thank you.

Community
  • 1
user1045845
  • 51
  • Assume G is connected and H is a spanning tree. Then could you do the problem? – Ncat Nov 15 '13 at 04:09
  • I do not understand the meaning of this proposition in the first place. That is why I was wondering the proof... :( – user1045845 Nov 15 '13 at 04:24
  • If you're having trouble parsing it, try looking up the words and symbols you don't know. What pieces of it do and don't you understand? – Ncat Nov 15 '13 at 04:27
  • i am having trouble trying to come up with an example of this proposition. because I do not under stand it in the first place. I understand better with proof. so i was wondering this website could help with the proof. – user1045845 Nov 15 '13 at 04:38

1 Answers1

1

Here's an example to illustrate what's going on:

example graph and spanning forest

By definition, a spanning forest is the union of a collection of vertex-disjoint trees that together span the original graph. Since a $t$-vertex tree has exactly $t-1$ edges (see e.g. this math.SE answer for a proof), an $n$-vertex $k$-component forest has $n-k$ edges.

Since $H$ is assumed to be a spanning forest, the second part only says $H$ is a tree if and only if it has $n-1$ edges.

Community
  • 1
Rebecca J. Stones
  • 27,246