How to find the equation of a line, tangent to a circle, that passes through a given external point

Question

I am given the equation of a circle: $(x + 2)^2 + (y + 7)^2 = 25$. The radius is $5$. Center of the circle: $(-2, -7)$.

Two lines tangent to this circle pass through point $(4, -3)$, which is outside of said circle. How would I go about finding one of the equations of the lines tangent to the circle?

I haven't started calculus, so I ask for advice fitting for someone starting a topic like this.

Answer 1

A useful technique for this situation which avoids using calculus goes like this:

Find the equation of the line through the point $(4,-3)$ with gradient $k$, and then use this (linear) equation to substitute into the equation of the circle to get a quadratic. The two roots of this quadratic would give the 2 points of intersection of the line with the circle, but in our case, we want to know the values of $k$ for which the quadratic has a double root (i.e. the 2 points of intersection are actually coincident). Use the standard condition ($b^2=4ac$) for a double root of a quadratic.

In your case, the equation of the line through $(4,-3)$ with gradient $k$ is $y+3 = k(x-4)$, or $y+7 = k(x-4)+4$. Substituting this into the equation of the circle gives:

$$(x+2)^2 + (k(x-4)+4)^2 = 25$$

So you need to rearrange this quadratic in $x$ and find out which values of $k$ give double roots.

Answer 2

Without any loss of generality we can draw a tangent to a circle with centre $C\equiv(C_x,C_y)$ and radius $r$ and choose a point $P\equiv(P_x,P_y)$ on the tangent so that its distance from the centre is $\overline{CP}\equiv d$ with $d \ge r$.

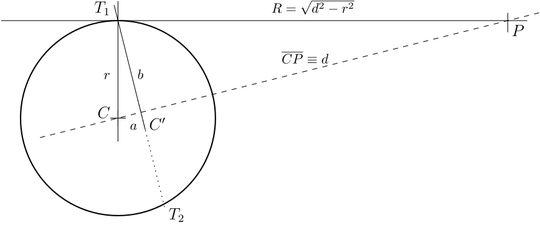
From the sketch above we recognize that the tangency points can be described as the sums of vectors, i.e.,

$$ \overrightarrow{OT_1} = \overrightarrow{OC}+ \frac{a}{d}\,\overrightarrow{CP}+ \frac{b}{d}\,\overrightarrow{CP}',\qquad \overrightarrow{OT_2} = \overrightarrow{OC}+ \frac{a}{d}\,\overrightarrow{CP}- \frac{b}{d}\,\overrightarrow{CP}'$$

where the prime in $\overrightarrow{CP}'$ represents a 90⁰ anticlockwise rotation of the vector.

Because our task is now to determine $a/d$ and $b/d$, we observe that the triangles $CT_1C'$ and $CPT_1$ are similar so that, with the position $\rho=r/d$, we have

$$\frac{a}{r} = \frac{r}{d} \implies \frac{a}{d}=\left(\frac{r}{d}\right)^2 =\rho^2$$

and

$$\frac{b}{r} = \frac{R}{d} \implies \frac{b}{d}=\frac{rR}{d^2} =\rho\frac Rd$$

but $R=\sqrt{d^2-r^2}$ and eventually we can write

$$ \frac{b}{d}= \rho\sqrt{1-\rho^2}.$$

From the last relation we recognize 1) that a real solution requires $\rho\le1$ (i.e., $P$ is not inside the circle) and 2) that for $\rho=1$ the point $P$ is on the circumference and the tangency points degenerate into $P$.

The OP can now compute the tangency points, etc.

E.g., in Python 3 (that is as close to pseudo-code as it could possibly be...)

from math import sqrt
# Data Section, change as you need #
Cx, Cy = -2, -7                    #
r = 5                              #
Px, Py =  4, -3                    #
# ################################ #
dx, dy = Px-Cx, Py-Cy
dxr, dyr = -dy, dx
d = sqrt(dx**2+dy**2)
if d >= r :
    rho = r/d
    ad = rho**2
    bd = rho*sqrt(1-rho**2)
    T1x = Cx + ad*dx + bd*dxr
    T1y = Cy + ad*dy + bd*dyr
    T2x = Cx + ad*dx - bd*dxr
    T2y = Cy + ad*dy - bd*dyr

    print('The tangent points:')
    print('\tT1≡(%g,%g),  T2≡(%g,%g).'%(T1x, T1y, T2x, T2y))
    if (d/r-1) < 1E-8:
        print('P is on the circumference')
    else:
        print('The equations of the lines P-T1 and P-T2:')
        print('\t%+g·y%+g·x%+g = 0'%(T1x-Px, Py-T1y, T1y*Px-T1x*Py))
        print('\t%+g·y%+g·x%+g = 0'%(T2x-Px, Py-T2y, T2y*Px-T2x*Py))
else:
    print('''\
Point P≡(%g,%g) is inside the circle with centre C≡(%g,%g) and radius r=%g.
No tangent is possible...''' % (Px, Py, Cx, Cy, r))

Executing the program yields

The tangent points:
    T1≡(-1.1139,-2.07914),  T2≡(2.88314,-8.0747).
The equations of the lines P-T1 and P-T2:
    -5.1139·y-0.920857·x-11.6583 = 0
    -1.11686·y+5.0747·x-23.6494 = 0

Answer 3

One possible approach would be the following:
1) Denote by $A$ the point $(4,-3)$, by $O$ the center of the circle, and by $P_1,P_2$ the two points on the circle in which the corresponding tangent line intersects the circle. Then both the triangles $AOP_1$ and $AOP_2$ are right, with hypotenuse $AO$.
2) The length of $AO$ is $\sqrt{(-2-4)^2+(-7-(-3))^2}=\sqrt{36+16}=\sqrt{52}$. The length of $OP_1$ and of $OP_2$ is the radius, and therefore equal to $5$. So, using the Pythagorean theorem, we get: $$|AP_1|=|AP_2|=\sqrt{|OA|^2-r^2}=\sqrt{52-25}=\sqrt{27}$$ 3) From here you can find both $P_1$ and $P_2$ - they are the points of intersections of the given circle with the circle of radius $\sqrt{27}$ around $(4,-3)$.
4) Now find the equations of two lines passing through given points.

Answer 4

My work out

1. PC gradient:

   (-3+7)/(4+2)=tan(33.7°)

2. PC distance:

   √((-3+7)²+(4+2)²)=√52

3. ∠CPQ = arcsin(5/√52)=43.9°

4. Equations of tangent passing through PQ & PR

   (Y+3)/(X-4)=tan(33.7±43.9)

Answer 5

We can use the formula for the distance from a point to a line. The distance between a line $ax + by + c = 0$ and a point $(x_0, y_0)$ is $$\left| \frac{a x_0 + b y_0 + c}{\sqrt{a^2+b^2}} \right|.$$

The line of tangency that passes the point $(4, -3)$ has equation $y+3 = m(x-4)$ for some slope $m$. So we just need to find $m$. Note that this equation can be written as $$mx - y -4m -3 = 0.$$

The distance between the center of the circle $(-2, -7)$ and the tangent line $mx - y -4m -3 = 0$ can be found from the formula above. This distance also equals to the radius of the circle, which is $5$. Hence

$$\left| \frac{m(-2) + (-1)(-7) +(-4m -3)}{\sqrt{m^2 + 1}} \right| = 5.$$ Rearranging we have $$|-6m + 4| = 5 \sqrt{m^2+1}. $$ Squaring and rearranging, we get the quadratic equation $$11m^2 - 48m - 9 = 0$$ with solutions $$m = \frac{24\pm15\sqrt{3}}{11}.$$

Therefore, the required equations for the tangent lines are $$y+3 = \frac{24+15\sqrt{3}}{11}\cdot(x-4)$$ and $$y+3 = \frac{24-15\sqrt{3}}{11}\cdot(x-4).$$

Answer 6

Assume the point where the tangent touches the circle is $(x_1,y_2)$, then this point satisfies the equation of the circle and the equation

$$ y'= \frac{y_1+3}{x_1-4 }\longrightarrow (*).$$

Now, you need to find $y'$ and evaluate it at the point $(x_1,y_1)$ and subs. back in (*), so you end up having two Equations in two variables. Solve them to find the point $(x_1,y_1)$ and finaly you will have two points that required to find the tangent plane.

Answer 7

The equation of any line passing through $(4,-3)$ is $$\frac{y+3}{x-4}=m\iff mx-y-4m-3=0$$ where $m$ is the gradient

Now, the perpendicular distance of tangent to center of circle = radius of circle

Do you know how to calculate the perpendicular distance of a line from the point?

Observe that the values of $m$

$(i)$ will be distinct real (hence, two tangents) if the point lies outside the circle,

$(ii)$ will be equal real (hence, one tangent) if the point lies on the circle,

$(iii)$ will be distinct imaginary (hence, no real tangents) if the point lies inside the circle,

See $12(b)$ here

Answer 8

Let $P(x,y)$ be one of the points at which a tangent line fron $Q(4,-3)$ to the circle $$(x+2)^2+(y+7)^2=25\tag 1$$ touches. Then $P(x,y)$ satifies the equation $(1)$ since it is on that circle. We need another equation to solve $x$ and $y$.

(Informal) Geometric meaning of the derivative: The derivative of a curve at a point is equal to the slope of the tangent line at that point: $m=y'$.

(Informal) Implicit Differentiation: If $F(x,y)=c$ then $y'=-\frac{F_x}{F_y}$ where $F_x$ and $F_y$ are partial derivatives.

Analytic geometry: The slope of the line passing through $P(x,y)$ and $Q(x_0,y_0)$ is $m=\frac{y-y_0}{x-x_0}$.

From the ingredients above, we have $$m=\frac{y-(-3)}{x-4}=-\frac{x+2}{y+7}=y'$$ or $$(x-1)^2+(y+5)^2=13.\tag 2$$ Now it is clear that $P$ is one of the intersection points of the circles $(1)$ and $(2)$. If we substract the equation $(2)$ from $(1)$ we find the radical axis $$y=-\frac32x-\frac{15}4\tag3$$ of these circles passing through the intersection points which are the tangency points we are looking for. Substituting $(3)$ in $(1)$ or $(2)$ we have $$52x^2-92x-167=0.\tag4$$

For the remaining computations I had to use WolframAlpha:

Solving $(4)$, WA finds that the $x$-coordinate of $P$ can be $$x=\frac{23}{26}\pm\frac{15\sqrt3}{13}$$ with the corresponding $y$-coordinates $$y=-\frac{66}{13}\mp\frac{45\sqrt3}{26}.$$ The tangent lines searched for are $$\frac{y+3}{x-4}=\frac{24\pm15\sqrt3}{11}.$$

Answer 9

Let eq of tangents be y= mx+ c then it passes through point (4,-3) So -3=4m+c let it put aside Now tangent touches circle so radius = distance between centre and line 5 = |-2m+7+c|/(m^2+1)^1/2 By solving we get 11 m^2 +24m=9 We get two values of m These are slopes of linesenter preformatted text here We can equation of lines and angle between lines This is my idea