Why is this below working hard?$$\int_{-\infty}^\infty \arctan(e^x)\arctan(e^{-x})dx\overset{e^{x}\to x}=\int_0^\infty \frac{\arctan x }{x}\arctan\left(\frac{1}{x}\right)\,dx$$
$$\arctan x=\sum _{k=0}^{\infty }{\frac {(-1)^{k}x^{2k+1}}{2k+1}}\implies \arctan\left(\frac{1}{x}\right)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}x^{-(2k+1)}}{2k+1}}$$
$$\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2k+1}}\int_0^\infty \frac{\arctan x }{x^{2k+2}}\,dx$$
The main issue is in this method failing because of the below integral being divergent,
$$\int_0^\infty \frac{\arctan x }{x^{2k+2}}\,dx$$
If I tried the other way,
$$\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2k+1}}\int_0^\infty x^{2k}{\arctan\left(\frac{1}{x}\right)}\,dx=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2k+1}}\int_0^\infty \frac{\arctan x }{x^{2k+2}}\,dx$$
We get the same thing.
There is a tiny window of convergence though but no generalization exists.
The below formula is valid for $p \in (-2,-1)$
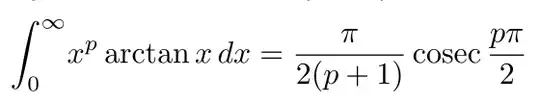
I do know how to solve the integral using alternate methods, but I'm interested to see if we can continue this work.
The closed form is,
$$\int_{-\infty}^\infty \arctan(e^x)\arctan(e^{-x})dx=\frac74 \zeta(3)$$
To save you time, my main hurdle is the integral being generalized only and not the series formed afterwards.
I do believe that the interchange of $\sum\iff \int$ is wrong I think? Fubini fails? Is this the main problem?
Edit :
$$\int_0^\infty \frac{\arctan x }{x^{2k+2}}\,dx=\int_0^1 \frac{\arctan x }{x^{2k+2}}\,dx+\int_1^\infty \frac{\arctan x }{x^{2k+2}}\,dx$$
For the second integral,
$$\int_1^\infty \frac{\arctan x }{x^{2k+2}}\,dx \underset{x\to 1/x}\implies \frac{\pi}{2}\int_0^1 x^{2k}\,dx - \int_0^1 x^{2k}\arctan x \, dx$$
So,
$$\int_0^1 \frac{\arctan x }{x^{2k+2}}\,dx+\frac{\pi}{2}\int_0^1 x^{2k}\,dx - \int_0^1 x^{2k}\arctan x \, dx$$
I feel physical pain in just imagining to solve a series with Dirichlet Beta function in it.
And, we get another integral to worry about $\int_0^1 \frac{\arctan x }{x^{2k+2}}\,dx$.
I believe this entire method will end up in a very difficult series which nicely boils down to $\frac74\zeta(3)$.