1

Problem

A trapezoidal prism is "cut" by an infinite plane. The plane passes through the center of the trapezoidal prism, and the normal vector to the plane is known. The prism is isosceles (meaning its trapezoidal faces are isosceles). I wish to determine or approximate the surface area of the intersection in a computationally efficient manner.

What I've Tried

I have already determined a "brute force" method for accomplishing this, however it is far too computationally expensive for my purposes (I need to perform this operation on the order of $10^7$ to $10^{10}$ times). I suspect that, especially given the symmetries and simplifying assumptions I'm able to make (isosceles prism, plane passes through center) that there's a far simpler method if not some analytic or near-analytic formula. Here's what I'm doing now:

  • Find Edge-Plane Intersections
    • Iterate over each edge of the prism. Compute the intersection point with the plane (if any) using parametric line-plane intersection formula.
    • Filter Valid Intersection Points Keep only those within edge bounds (0 ≤ t ≤ 1). Remove duplicates using a tolerance check.
  • Order Points to Form Polygon
    • Compute the centroid of intersection points.
    • Construct a local 2D basis (orthonormal to the plane normal).
    • Sort them by angle around the centroid to get polygon ordering.
  • Compute Polygon Area
    • Use the triangle fan method and 3D cross products.
    • Sum triangle areas formed by the ordered vertices.

Steps Toward a Solution

I've given this a considerable amount of thought, and I feel as though I'm tantalizingly close to a solution.

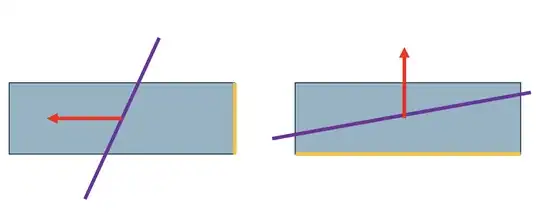
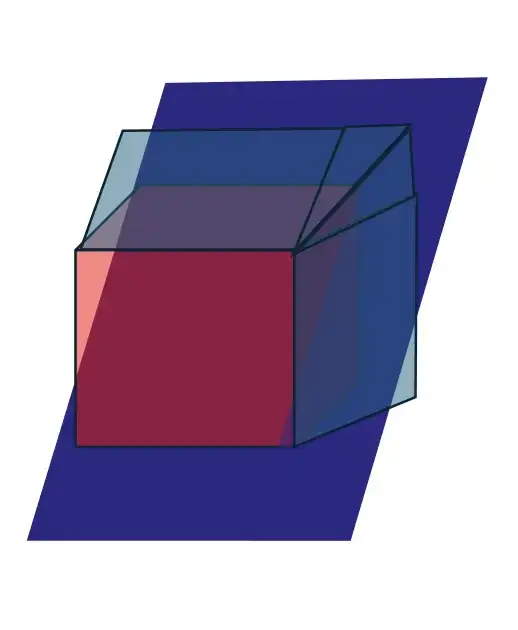
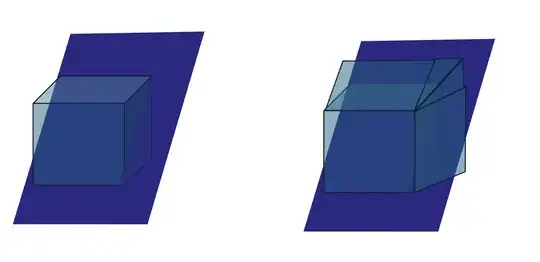enter image description here Figure 1. Planes intersecting a rectangular prism and a trapezoidal prism.

If instead of a trapezoidal prism, we were working with a rectangular prism, the solution becomes a bit simpler. We can project the polygon formed by the intersection onto one of the $x-y$, $x-z$, or $y-z$ plane by simply ignoring the third coordinate. Using the shoelace formula, we can then determine the area of this projected polygon. The surface are of the intersection is the area of the projected polygon divided by the cosine of the angle between the normal to the plane and the ignored axis.

enter image description here

This becomes even simpler in a handful of special cases, such as those depicted above, where the area of the projected polygon is simply the area of one of the faces. The angle between the normal and the ignored axis (let it be the $z$ axis) is simply:

$$\theta = \frac{\hat{n}\cdot\hat{z}}{|\hat{n}||\hat{z}|} = \hat{n}_z$$

So that the area of the intersection ends up being something as simple as:

$$\frac{\text{Area of face}}{\cos(\hat{n}_z)}$$

And in code I could perhaps do something simple like perform a check on the angle of the normal vector w.r.t. one of the axes to determine which face to use. There's more work to be done, but it seems plausible to me that I could come up with a simple formula for the surface area of the intersection of a cube.

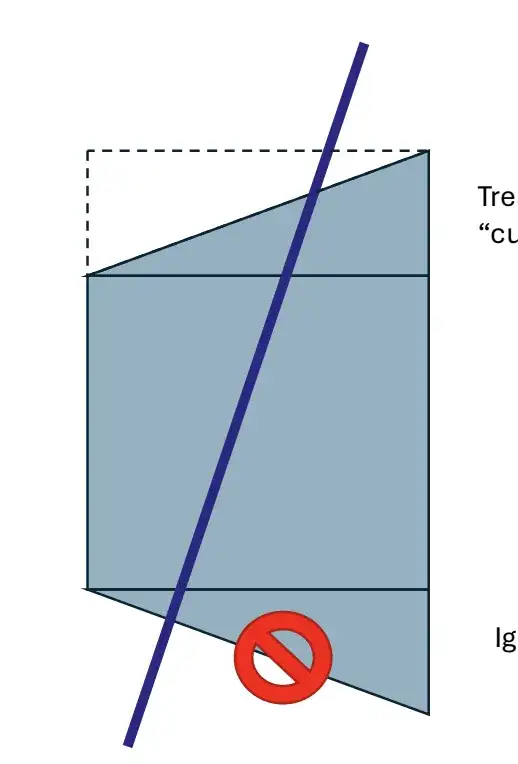
enter image description here

What I have, however, is a trapezoidal prism. I could break this trapezoidal prism up into a rectangular prism (for which the intersectional surface area may be easy to compute) and a set of wedges. I could perhaps make the approximation that the "corners" can be ignored.

Determining the surface area of the cross sections with the wedges seems difficult, but I suspect that I can treat these as rectangular prisms as well. Notice that (I think) the sum of the surface area of the cross sections of the plane with the wedges at top and bottom drawn here is the same as the surface area of the cross section of the rectangular prism drawn with the dotted line.

enter image description here

It has also been suggested to me that I could use Cauchy's surface area formula. I am not familiar with this, however, and my reading has not made it obvious to me how this formula could be applied.

Is there a simpler/more computationally efficient way to determine or approximate the surface area of the intersection?

IntegerEuler
  • 53
  • Have you considered Monte Carlo? Enclose the prism in a cube one of whose faces is parallel to the infinite plane. Area of the intersection of the plane with this cube is trivial. The area that you want is the above area multiplied by the probability that a random point in the intersection of plane with cube is also in the intersection with the prism. This probability can be estimated using Monte Carlo. – Jayanth R Varma Jun 27 '25 at 08:31
  • What do you mean by "the center of the prism"? – mr_e_man Jun 30 '25 at 18:09
  • @mr_e_man The point is equidistant from any two opposing faces. If the prism was placed in a Cartesian coordinate system so that one corner coincided with the origin, and one face coincided with the $xy$ plane, the coordinate of the point would be $(h/2, w/2, l/2)$ for a prism of height $h$, width $w$, and length $l$. (Hopefully that's clear; I'll add an image soon) – IntegerEuler Jun 30 '25 at 23:53
  • That only works for rectangular prisms, not isosceles trapezoidal prisms in general. – mr_e_man Jun 30 '25 at 23:55
  • I mean, "height, width, length" only makes sense for rectangular prisms. But "equidistant from opposing faces" does make sense in general. – mr_e_man Jun 30 '25 at 23:58

1 Answers1

2

If I'm not mistaken, I think the idea of projection works.

Let $ABCD-EFGH$ be our trapezoidal prism where $ABCD$ and $EFGH$ are congruent trapezoids.
(This answer assumes that each of $EA,FB,GC,HD$ is perpendicular to the plane $ABCD$.)

Let $P$ be our plane.

  • Case 1 where the trapezoid $ABCD$ has intersection points with $P$, and the trapezoid $EFGH$ does not have intersection points with $P$.
    Let us consider the following example : trapezoidal prism and a plane
    Let $I,J,K,L,M,N$ be the intersection point of $P$ with $AE,BF,CG,DH,BC,CD$ respectively.
    Now, let us consider the projection of these points to the plane $ABCD$.
    Then, since $I'=A,J'=B, M'=M$, etc, we see that $\text{area}(I'J'M'N'L')$ is equal to $\text{area}(ABMND)$ which is easy to find.

  • Case 2 where neither $ABCD$ nor $EFGH$ has intersection points with $P$.
    Using the idea in Case 1, we have $$\text{area}(I'J'K'L')=\text{area}(ABCD)$$

  • Case 3 where both trapezoids $ABCD$ and $EFGH$ have intersection points with $P$. It should be easy to find the area of the intersection since the intersection is either a quadrilateral or a triangle.

mathlove
  • 151,597