Intuition behind homotopy $\alpha \star (\beta \star \gamma) \simeq (\alpha \star \beta) \star \gamma$

Question

I'm learning algebraic topology and in the notes I'm reading I've encountered the following result:

Let $X$ be a topological space, $p,\ q,\ r,\ s \in X$ and $\alpha \in \Omega_{p,q}(X),\ \beta \in \Omega_{q, r}(X),\ \gamma \in \Omega_{r,s}(X).$ The following propoerties are true:

1. $\alpha \star(\beta\star\gamma) \simeq (\alpha \star \beta) \star \gamma$
2. $\epsilon_{p} \star \alpha \simeq \alpha \star \epsilon_{q} \simeq\alpha $
3. $\alpha \star \bar{\alpha} \simeq \epsilon_{p}$

Now, the proof for $(1)$ reads like this:

The homotopy $H:[0,1]^{2} \to X$,

$$ H(t,s) = \cases{ \alpha(\frac{4t}{2-s}),\ \ t \in [0, \frac{2-s}{4}]\\ \beta(4t+s-2),\ \ t \in [\frac{2-s}{4}, \frac{3-s}{4}]\\ \gamma(\frac{4t+s-3}{s+1}),\ \ t \in [\frac{3-s}{4}, 1] } $$

proves that $\alpha \star (\beta \star \gamma) \simeq (\alpha \star \beta) \star \gamma$.

My question is how does one come up with that formula. Because I can check that it works, but I think it's more important learning how to construct the homotopy.

Answer 1

The key insight is this picture:

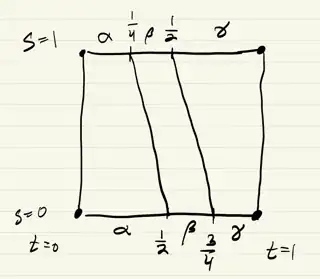
The $s=0$ part of the homotopy (the bottom edge of the square) is the path $\alpha \star (\beta \star \gamma)$, and the $s=1$ part of the homotopy (the top edge of the square) is the path $(\alpha \star \beta) \star \gamma$. On a particular slice $s=s_*$ we have the path that squeezes $\alpha$ into the first section, $\beta$ into the second, and $\gamma$ into the third section, where these sections have lengths $\ell_1$, $\ell_2$, and $\ell_3$ as shown here:

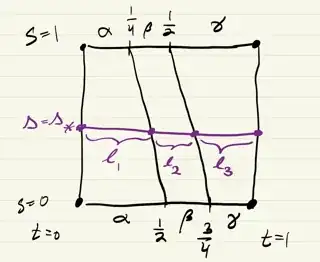
Now it's easy to see what our path should be at $s=s_*$, since we have to make $\alpha,\beta,\gamma : [0,1] \to X$ fit into intervals (respectively) $[0,\ell_1] \to X$, $[\ell_1, \ell_1 + \ell_2] \to X$, and $[\ell_1 + \ell_2, 1] \to X$. We do this by just rescaling and shifting our intervals -- for instance to get from $[\ell_1, \ell_1 + \ell_2]$ to $[0,1]$ (so we can plug into $\beta$) we first subtract off $\ell_1$ to get $[0, \ell_2]$ then we divide by $\ell_2$ to get $[0,1]$. This tells us to use $\beta(\frac{t-\ell_1}{\ell_2})$, and so in general we get a path

$$ H(s_*,t) = \begin{cases} \alpha(\frac{t}{\ell_1}) & t \in [0,\ell_1] \\ \beta(\frac{t-\ell_1}{\ell_2}) & t \in [\ell_1, \ell_1 + \ell_2] \\ \gamma(\frac{t - \ell_1 - \ell_2}{\ell_3}) & t \in [\ell_1 + \ell_2, 1] \end{cases} $$

Now all that's left is to figure out what $\ell_1, \ell_2, \ell_3$ are for any given $s$. But we know that $\ell_1$, for instance, is the $t$ coordinate on the line connecting $(s=0,t=\frac{1}{2})$ to $(s=1,t=\frac{1}{4})$, so we find the equation of this line and solve for $t$ as function of $s$ to get $\ell_1 = \frac{2-s}{4}$. We can play the same game for $\ell_2$, but it's clear from the picture that $\ell_2 = \frac{1}{4}$ is constant. Lastly we compute $\ell_3 = 1 - (\ell_1 + \ell_2)$, so that we have

• $\ell_1(s) = \frac{2-s}{4}$
• $\ell_2(s) = \frac{1}{4}$
• $\ell_3(s) = \frac{1+s}{4}$

This tells us our homotopy should be

$$ H(s_*,t) = \begin{cases} \alpha(\frac{t}{\frac{2-s}{4}}) & t \in [0,\frac{2-s}{4}] \\ \beta(\frac{t-\frac{2-s}{4}}{\frac{1}{4}}) & t \in [\frac{2-s}{4}, \frac{2-s}{4} + \frac{1}{4}] \\ \gamma(\frac{t - \frac{2-s}{4} - \frac{1}{4}}{\frac{1+s}{4}}) & t \in [\frac{2-s}{4} + \frac{1}{4}, 1] \end{cases} $$

Of course, it's easy to see that simplifying these expressions gives the homotopy you were interested in.

Lastly, you can use similar pictures in order to explain the other homotopies on your list. First, it might be worth trying to draw these pictures yourself, but if you get stuck I'll include them under the cut. It makes a nice exercise to use these in order to derive your other homotopies from scratch!

---

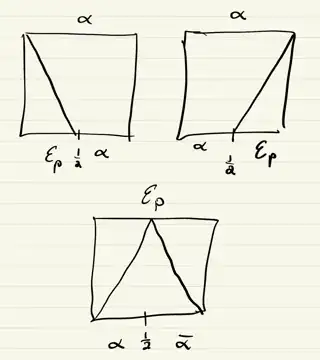
I hope this helps ^_^

Answer 2

The path $\alpha \star(\beta\star\gamma)$ moves

1. The first half of the time $[0,1/2]$ along $\alpha$. (twice the original "velocity")

2. The second half of the time $[1/2,1]$ along $\beta\star\gamma$. In this second half

• 2.1. The first half of the interval [1/2,3/4] it moves along $\beta.$ (four times the original velocity)

• 2.2. The second half of the interval [3/4,1] it moves along $\gamma.$ (four times the original velocity)

On the other hand the path $(\alpha \star \beta) \star\gamma$ moves

1. The first half of the time $[0,1/2]$ along $\alpha \star \beta$. In this first half

• 1.1. The first half of the interval $[0,1/4]$ it moves along $\alpha.$ (four times the original velocity)

• 1.2. The second half of the interval $[1/4,1/2]$ it moves along $\beta.$ (four times the original velocity)

2. The second half of the time $[1/2,1]$ along $ \gamma$. (twice the original velocity)

So you move along both paths $\alpha$, $\beta$ and $\gamma$ in the same order but different velocities. To do the homotopy you continuously change with $s$ the velocity we cover $\alpha$, $\beta$ and $\gamma$ from velocities $2x$, $4x$, $4x$ at $s=0$ to $4x$, $4x$, $2x$ at $s=1.$

• For fixed $s$ the map $\displaystyle \frac{4t}{2-s}$ maps the interval $[0,\frac{2-s}{4}]$ to $[0,1]$ with derivative $\frac{4}{2-s}$. So for $s=0$ the derivative is $2$ and for $s=1$ the its derivative is $4$.

• For fixed $s$ the map $\displaystyle 4t+s-2$ maps the interval $[\frac{2-s}{4},\frac{3-s}{4}]$ to $[0,1]$ with derivative $4$. So for every $s$ its derivative is $4$.

• For fixed $s$ the map $\displaystyle \frac{4t+s-3}{s+1}$ maps the interval $[\frac{3-s}{4},1]$ to $[0,1]$ with derivative $\frac{4}{1+s}$. So for $s=0$ the derivative is $4$ and for $s=1$ the its derivative is $2$.

In other words for every fixed $s$ the path $t\mapsto H(t,s)$ is just a reparametrization of the initial path $\omega=\alpha \star(\beta\star\gamma)$ moving along at different "speeds", that is $H(t,s)=\omega(\theta_s(t)),$ where $\theta_s\colon [0,1]\rightarrow [0,1]$ is the homeomorphism

$$\theta_s(t):=\begin{cases}\displaystyle \frac{2t}{2-s}, & t\in [0,\frac{2-s}{4}],\\ \displaystyle t+s/4, & t\in [\frac{2-s}{4},\frac{3-s}{4}],\\ \displaystyle 3/4+\frac{t+s/4-3/4}{s+1}, & t\in [\frac{3-s}{4},1]. \end{cases} $$

Answer 3

The intuition is that the LHS and the RHS just represent the same curve. That is, their images are the same, and the directions in which you traverse these images are the same; the difference is only in the speed with which you traverse. Homotopically, the speed does not matter, as a change of the speed corresponds to a stretching of the domain interval. After all, you could have defined path spaces via maps from $[0,2]$ instead of $[0,1]$, or define $\star$ with the same formula but using $[0,1] = [0, 1/3] \cup [1/3, 1]$ instead of $[0,1] = [0, 1/2] \cup [1/2, 1]$. This is all arbitrary and does not matter, which is the only lesson worth the time here, I believe.

If you still really want to write formulas, the idea of the speed change seems sufficient. You know that in $\alpha \star(\beta\star\gamma)$ the speed of $\alpha$ is only twice the initial one (as only one $\star$ gets to act on it), and the speed of $\beta$ and $\gamma$ is $4$ times the initial one, while in $(\alpha \star \beta) \star \gamma$, the curve $\gamma$ has twice the speed, and $\alpha$ is sped up $4$ times. Then to connect them, you have to speed up $\alpha$ and slow down $\gamma$. Thus you add this $\frac{1}{2-s}$ to the formula of $\alpha$ -- it goes from $\frac{1}{2}$ when $s=0$ to $1$ when $s=1$. And similarly, $\frac{1}{s+1}$ in $\gamma$'s part of the formula goes from $1$ to $\frac{1}{2}$. The rest of the formula just makes sure that the three subintervals ''belonging'' to $\alpha, \beta, \gamma$ don't overlap and cover $[0,1]$.