Character table of semidirect product of $\mathbb{Z}/7\mathbb{Z}$ with $\mathbb{Z}/3\mathbb{Z}$

Question

I am trying to compute the character table of $\mathbb{Z}/7\mathbb{Z} \rtimes \mathbb{Z}/3\mathbb{Z}$ given by $bab^{-1}=a^2$, where $a$ is the generator of $\mathbb{Z}/7\mathbb{Z}$ and $b$ the generator of $\mathbb{Z}/3\mathbb{Z}$.

I already have the following information and want to find $x$ and $y$. I tried using the ortogonality of columns to get $x+y=-1$ and $|x|^2+|y|^2=4$.

Edit: I am thinking more in the direction of using that the conjugate of an irreducible character is also irreducible. If I somehow get to show that $x,y\in \mathbb{R}$ the table follows directly from the relations above, but I don't know how to show that $x,y$ are not complex.

Answer 1

It's actually not that hard to compute the two irreducible representations of dimension $3$. Let $\rho$ be such a representation. Since $\rho(a)$ is similar to $\rho(a^2)=\rho(a)^2$, by spectral mapping theorem, the spectrum $\sigma(a)$ of $\rho(a)$ is closed under squaring. If $\sigma(a)=\{1\}$, then $a=I_3$, the representation must be reducible. Therefore $\sigma(a)$ contains a primitive $7$th root of $1$, say $\zeta$, then it also contains $\zeta^2, \zeta^4$ which are all distinct, hence they must be all of $\sigma(a)$. And by $bab^{-1}=a^2$, $\rho(b^{-1})$ sends the eigenspaces $E_{\zeta}, E_{\zeta^2}, E_{\zeta^4}$ to $E_{\zeta^2}, E_{\zeta^4}, E_{\zeta^8}=E_{\zeta}$ respectively. So under $\{v, b^{-1}v, b^{-2}v\}$ for any nonzero $v\in E_{\zeta}$, we have

$$\rho(a) = \begin{pmatrix} \zeta & & \\ & \zeta^2 & \\ & & \zeta^4\end{pmatrix}, \rho(b^{-1}) = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}$$

This must be irreducible, because $\rho(a), \rho(b^{-1})$ don't commute, hence cannot be decomposed as direct sum of one dimensional representations.

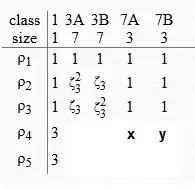
In particular, the last two rows are of the form $[3, 0, 0, *, *]$.

---

We can compute $x,y$ by picking $\zeta$, but we'd rather finish by orthogonality relations. The orthogonality of 1st and 4th row gives $x+y=-1$. And the inner product of the 4th row with itself gets us $|x|^2+|y|^2=4$.

If one of $x,y$ are real, then by $x+y=-1$, they are both real, moreover

$$\begin{cases} x^2+y^2=4 \\ x+y=-1 \end{cases}\Rightarrow xy=\frac{(x+y)^2-(x^2+y^2)}{2}=-\frac{3}{2}$$

But $x,y$ must be algebraic integers, so must be $xy$.

Thus $x,y$ are both imaginary, and since the Galois conjugate of an irreducible representation is still irreducible, we have the last row ends with $\bar x, \bar y$.

---

There is an outer automorphism $f$ of $G=\Bbb Z/7\Bbb Z\rtimes\Bbb Z/3\Bbb Z$: $f(a)=a^3, f(b)=b$.

As $\rho_4$ is irreducible, so is $\rho_4\circ f$, hence $\rho_4\circ f$ is isomorphic to $\rho_4$ or $\rho_5$. Since $f$ interchanges the classes $7A$ and $7B$, the character of $\rho_4\circ f$ can be obtained by switching $x,y$. Hence $\rho_4\circ f\simeq \rho_4$ iff $x=y$ which is incompatible with $x+y=-1, |x|^2+|y|^2=4$. Therefore $\rho_4\circ f\simeq \rho_5$, and the last row must end up with $y, x$.

Thus we must have $x=\bar y$, and $|x|^2+|y|^2=4$ implies $xy=2$.

So $$\begin{cases} xy = 2 \\ x+y=-1 \end{cases}\Rightarrow x, y = \frac{-1\pm \sqrt{-7}}{2}$$

Answer 2

The fact that the remaining characters have degree $3$ suggests that it might be a good idea to induce a few characters from an index $3$ subgroup and see what happens. In this case you have only one index $3$ subgroup. Inducing a trivial character from a proper subgroup never gives an irreducible character (by Frobenius reciprocity that induction will always have a trivial character as a summand), so it seems like a good idea to induce a non-trivial character.

I will let you take it from there. After you have completed this character table, have a look at this (I highly recommend that you do your special case first): Classifying the irreducible representations of $\mathbb{Z}/p\mathbb{Z}\rtimes \mathbb{Z}/n \mathbb{Z}$.

Answer 3

I think that @Just a user's solution is exactly what is needed.

I only offer this to show an alternative which uses an argument [see (iv) below] which is useful in other situations.

Rather than concentrate on rows I'd look at columns.

(i) As the length of the second and third columns are $3$ we have that $\rho_4$ and $\rho_5$ are zero on the elements of order $3$.

Now suppose that the fourth column is $(1,1,1,\alpha,\beta)^T$.

(ii) By the orthogonality of the first and fourth columns we have that $$ \alpha+\beta=-1. $$

(iii) As the fourth column has length $7$ we have that $$ \alpha\bar{\alpha}+\beta\bar{\beta}=4. $$

(iv) As there are no conjugates $z^g,z^h$ of an element $z$ of order $7$ such that $z^g z^h=1$ we have that $$ \frac{|G|}{|C_G(z)||C_G(z)|}\sum_{i=1}^5\frac{\rho_i(z)\rho_i(z)\overline{\rho_i(1)}}{\rho_i(1)}=0, $$ or $$ \alpha^2+\beta^2=-3. $$

(v) From (iv) it is now clear that $\alpha$, $\beta$ cannot be real. Hence there is an irreducible got by conjugating $\rho_4$, and this must be $\rho_5$. That is $$ \beta=\bar{\alpha}. $$

(vi) From (iii) we now see that $$ \alpha\beta=2. $$

(vii) From (ii) and (vi) we now see that $\alpha, \beta$ are the roots of $$ \alpha+\frac{2}{\alpha}=-1, $$ that is, we can take $$ \alpha=\frac{-1+\sqrt{-7}}{2}, \beta=\frac{-1-\sqrt{-7}}{2}. $$

(viii) The same argument applies, of course to the fifth column, and since it cannot be equal to the fourth column, it must be $(1,1,1,\beta,\alpha)^T$.

Answer 4

Row orthogonality for characters of representations: Let $\chi_i,\chi_j$ be two characters of G. Then, $$\langle\chi_i,\chi_j\rangle=\frac1{|G|}\sum_{g\in G}\chi_i(g)\overline{\chi_j(g)}=\cases{1,&if $\chi_i=\chi_j$\\0,&if $\chi_i\neq\chi_j$}$$

Coloumn orthoganility for characters of representations: Let $S=\{\chi_1,\chi_2,...,\chi_r\}$ be the set of all characters of G. Then, $$\sum_{i=1}^r\chi_i(g)\overline{\chi_i(h)}=\cases{|C_G(g)|,&if $g$ and $h$ are conjugate\\\hspace{0.5cm}0\hspace{0.7cm},&otherwise}$$

Notation (According to M. Kubat): $\chi_i$ is the character of the representation $\rho_i$.

Suppose that the fourth row is: $$\array{3 &u &v &x &y}$$ From the given table in OP, if we consider the row orthogonaility relations $\langle\chi_4,\chi_i\rangle=0$ for $i=1,2,3$ and add these equations we get $$x+y=-1.\tag1$$

If we consider the coloumn orthogonality relations for the first and the $i$-th column, $i=2,3,4,5$, we find the $5$-th row: $$\array{3 &-u &-v &-1-x &-1-y}.$$

Then, from the second and the third columns orthoganility, we get $u\overline v=0.$ Hence, $u=v=0.$

Finally, from the forth and the fifth columns orthogonality, we get $$4+x+\overline y+2x\overline y=0.\tag2$$ Just a user's previous answer was wrong and deceived me. I thank him for telling me this. I think the trick is to see that $y=\overline x$ since the orthogonality relations are not enough.

Another way. If we consider the product of the coset $7A=\{a,a^2,a^4\}$ with itself, we see that $$\rho_4\otimes\rho_4=\rho_4\oplus2\rho_5\tag3$$ In fact the complex represantation ring of the group is generated by $\rho_2,\rho_4,\rho_5$, subject to the relations $\rho_2 ^3=1,$ $\rho_4 ^2=\rho_4+2\rho_5$, $\rho_5 ^2=2\rho_4+\rho_5$, $\rho_4\rho_5=\rho_4+\rho_5+3$, etc. By evaluating the relation $(3)$ at $a$ and taking its character, we get $$x^2=x+2(-1-x)$$ $$x^2+x+2=0$$ $$x=\frac{-1\pm i\sqrt7}2.$$