Why does closing the triangle over $y=e^{-x}$ lead to negative area?

Question

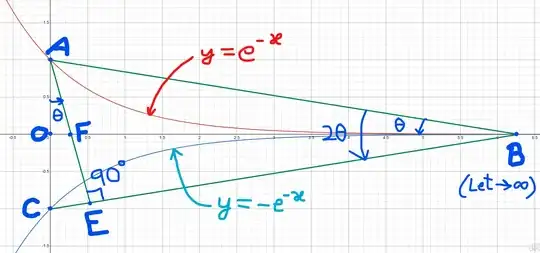
Consider the exponential decay curve $y = e^{-x}$, which starts at the point $A = (0,1)$ and approaches the $x$-axis as $x \to \infty$. The total area under this curve from $x = 0$ to $\infty$ is known to be:

$$ \int_0^\infty e^{-x} \, dx = 1. $$

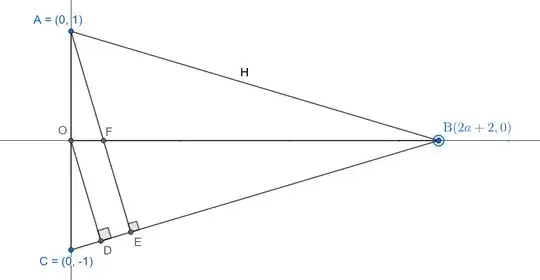
Now, imagine forming a triangle $\triangle AOB$, where:

• $O = (0,0)$ (the origin),
• $A = (0,1)$ (the curve's initial point),
• $B = (\to\infty, 0)$ ,
• and segment $AB$ connects $A$ directly to the tail of the curve, forming a closed triangle.

Let us assume that the area of triangle $AOB$ is the area under the curve (which is 1) plus some extra area $a$. So:

$$ \text{Area}_{\triangle AOB} = 1 + a. $$

Also, since triangle $AOB$ is right-angled at $O$, its area can also be written as:

$$ \text{Area} = \frac{1}{2} \cdot AO \cdot OB = \frac{1}{2} \cdot 1 \cdot OB = \frac{OB}{2}. $$

Equating both expressions for the area:

$$ 1 + a = \frac{OB}{2} \Rightarrow OB = 2a + 2. $$

Let $H = AB$ be the hypotenuse. Then, by Pythagoras Theorem:

$$ H^2 = AO^2 + OB^2 = 1^2 + (2a + 2)^2 = 4a^2 + 8a + 5. $$

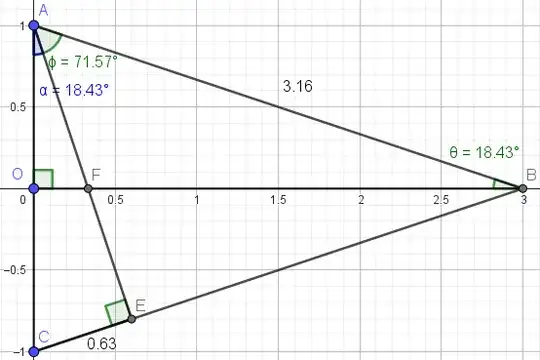
Consider a point $C = (0, -1)$ to which we join $B$ and form triangle $\triangle COB$. Now in triangle $ACB$, draw a perpendicular $AE$ onto the base $CB$. Let $AE$ intersect $OB$ at a point $F$.

Let $\theta$ be the angle $\angle ABO$. Since triangle $AOB$ is right-angled at $O$, we know:

$$ \angle ABO = \theta, \quad \angle CAB = 90^\circ - \theta. $$

Notice that in triangle $ACB$, $AB=BC$ and therefore:

$$ \angle ABO = \angle CBO = \theta $$ $$ \angle ABC = 2\theta $$

Now observe triangle $AEB$ — the full angle at $A$ becomes:

$$ \angle CAB = \angle CAE + \angle EAB. $$

Also, from triangle $AEB$:

$$ \angle EAB = 90^\circ - 2\theta. $$

So:

$$ \angle CAE = \angle CAB - \angle EAB = 90^\circ - \theta - (90^\circ - 2\theta) = \theta $$

Hence,:

$$ \boxed{\angle CAE = \angle ABO = \theta} $$

---

Now, using trigonometry in triangle $AOB$:

$$ \sin \theta = \frac{AO}{AB} = \frac{1}{H}. $$

In triangle $ACE$, we also have:

$$ \sin \theta = \frac{CE}{AO+OC} = \frac{CE}{1+1} \Rightarrow CE = 2\sin\theta= \frac{2}{H}. $$

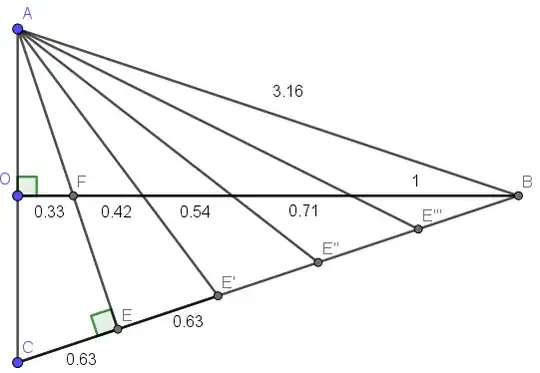
So the small segment $CE$ is known. Now:

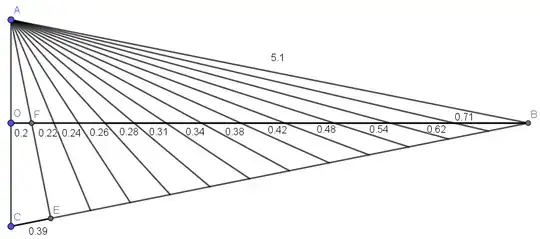
• We project $n$ number of line segments from $A$ onto $CB$ such that they divide $CB$ into equal lengths, each equal to $CE = \frac{2}{H}$.
• The first line segment is the perpendicular $AE$ itself.
• The final line segment is $AB$ that lands on $B$.
• Also observe that these $n$ number of line segments also divide $OB$ into equal lengths, each equal to $OF$.

Hence, the total number of such projections on $CB$ is:

$$ n = \frac{CB}{CE}. $$

But triangle $\triangle ABC$ is isosceles, with $AB = BC = H$, so:

$$ n = \frac{H}{2/H} = \frac{H^2}{2}. $$

Now let’s examine the segment $OB = 2a + 2$, and again recall from triangle $AOB$:

$$ \tan \theta = \frac{AO}{OB} = \frac{1}{2a + 2}. $$

In triangle $AOF$, which is right-angled at $O$, we also have:

$$ \tan \theta = \frac{OF}{AO} = OF/1. $$

Equating both expressions:

$$ OF = \frac{1}{2a + 2}. $$

As discussed before, the $n$ number of projections also divide $OB$ into equal lengths of $OF$. Therefore:

$$ n = \frac{OB}{OF} = \frac{2a + 2}{1/(2a + 2)} = (2a + 2)^2. $$

Equating this to the previous value of $n$:

$$ \frac{H^2}{2} = (2a + 2)^2. $$

We had:

$$ H^2 = 4a^2 + 8a + 5. $$

Substitute:

$$ \frac{4a^2 + 8a + 5}{2} = (2a + 2)^2. $$

Multiply both sides by 2:

$$ 4a^2 + 8a + 5 = 8a^2 + 16a + 8. $$

Bring all terms to one side:

$$ 0 = 4a^2 + 8a + 3 \Rightarrow a^2 + 2a + \frac{3}{4} = 0. $$

Solving:

$$ \boxed{a = -\frac{1}{2}, \quad a = -\frac{3}{2}} $$

But $a$ was introduced as the additional area beyond the area under the exponential curve — hence it must be non-negative.

Therefore, this contradiction suggests that trying to "close" the triangle over the exponential curve leads to negative area, which is geometrically invalid.

And what's more absurd is that if we respectively put these two negative values of $a$ in $OB=2a+2$, we get $OB=+1,-1$, which is impossible since $OB\to\infty$.

---

Conclusion / Open Question:

Why does this contradiction emerge? Is it because the asymptote at $y = 0$ can never be "closed" into a triangle using finite Euclidean geometry? Or did we just prove that the exponential curve never touches the asymptote?

I'd love to know how others interpret this contradiction geometrically or analytically.

Answer 1

The main point

Why does this contradiction emerge?

The contradiction emerges primarily from a misguided claim in the trigonometry calculations towards the end. Specifically, the following is not true:

these $n$ number of line segments [which divide $CB$ into equal lengths] also divide $OB$ into equal lengths, each equal to $OF$

This can easily be seen in a to-scale diagram with $B=\left(3,0\right)$, which forces $n=5$:

That incorrect assumption is expressed as the key incorrect equation $n=\dfrac{OB}{OF}$, which causes the problems with $a$.

Infinity?

The question seems to hope that it is fine to take $B=\left(\infty,0\right)$ and to do geometry as normal. There is no way to do that that I or several commenters know about.

However, if there were a promising calculation where $\infty$ would seem to lead to a significant quantity different from $0$ (e.g. $a_{\left(\infty,0\right)}\overset{?}{=}-1/2\ne0$, or $\arctan\infty\overset{?}{=}\pi/2$), then one would typically expect/hope that we could get close to that value by replacing $\infty$ with a large real value (e.g. $\arctan\left(999\right)\approx\pi/2$, maybe $a_{\left(999,0\right)}\approx-1/2$). So I think there should be no harm in taking $B=\left(b,0\right)$ where $b$ is some large real number.

The one big question is whether taking a limit as $b$ tends to $\infty$ would somehow allow us to avoid the main error mentioned above: would those segments of $OB$ approach being equal in length to $OF$ as $b$ gets very large? Unfortunately, the answer is no: The ratio of the largest segment to the smallest increases as $b$ increases from $3$ to $5$.

The extreme ratio changes from about $1/0.33\approx3$ to $0.71/0.2\gtrsim3.5$. This suggests that taking $b$ to be some huge value would not mean that things are well-approximated by assuming the segments along $OB$ are equal.

Details and other errors

Initial Setup

The work does not seem to actually use $B=\left(\infty,0\right)$ anywhere, so I will assume $B=\left(b,0\right)$ for some $b>2$ so that the area of the triangle $AOB$ is greater than $1$, and thus it can be written in the form $1+a$ for some $a>0$.

Under this setup, it is true that $b=OB=2a+2$ (so that $a=\dfrac{b-2}{2}$). And it is true that for the hypotenuse of length $H$ we have $H^{2}=4a^{2}+8a+5$. And since $B$ is a real point, there is nothing wrong with drawing the altitude $AE$ from $A$ to $CB$ where $C=\left(0,-1\right)$, and intersecting it with $OB$ at $F$.

Angle typos

Let $\theta$ be the angle $\angle AOB$...

Given the context of the right angle at $O$ and the later work, this (and a repetition later) seems to be a mostly-minor typo for "$\angle OAB$". We could define $\theta:=\angle OAB$ so that $\angle ABO=90^{\circ}-\theta$ as written. However, for nearly all future work, it seems that $\theta$ was assumed to represent $\angle ABO$, which doesn't cause a big problem, but does cause a disconnect with this initial $\angle ABO=90^{\circ}-\theta$ equation.

So instead, let us take $\theta:=\angle ABO$ so that $\angle OAB=90^{\circ}-\theta$.

$\angle CAB=\angle CAB+\angle EAB$ is correct either way.

Also, from triangle $AEB$: $\angle EAB=90^{\circ}-2\theta$.

This is true with our corrected convention of $\theta=\angle ABO$.

But then we need to correct the next calculation which was based on a mixture of the two conventions:

$\angle CAE=\angle OAB-\angle EAB=90^{\circ}-\theta-\left(90^{\circ}-2\theta\right)=\theta$, not $3\theta-90^{\circ}$. The OP realized that $\angle CAE=\theta$ followed from symmetry anyway, and never actually used the value $3\theta-90^{\circ}$ again, so this correction doesn't make a difference.

Correcting the "$\angle AOB$" typo in the boxed equation, we have $\boxed{\angle CAE=\angle ABO=\theta}$.

(The calculations to show that $CE=\dfrac{2}{H}$ are fine.)

Many segments

For the next part, it seems that we are assuming that the length of $CB$ is an exact multiple of $CE$. If it's not an exact multiple, we could still draw segments until we run out of room in $CB$ for another copy of $CE$, but we may as well assume that we have an exact multiple.

Since $H=AB=CB$ is an exact multiple ($n$) of $CE=\dfrac{2}{H}$, we'd have $n=\dfrac{H^2}{2}$. Since $H^2=4a^2+8a+5$, we have $2n-5=4a(a+2)$. Since $1+a=\dfrac{b}{2}$, we have $4a(a+2)=4\left(\dfrac{b}{2}-1\right)\left(\dfrac{b}{2}+1\right)=(b-2)(b+2)=b^2-4$ as the integer $2n-5$. Therefore, $b^2=2n-1$.

So we will add the assumption that $b$ is the square root of an odd number, e.g. $b=\sqrt{5},$$\sqrt{7},3,\ldots$, which correspond to $n=3,4,5,\ldots$, respectively. (In general, $b=\sqrt{2n-1}$ so that $n=\dfrac{b^{2}+1}{2}$.)

Here are some illustrations for $\left(b,n\right)=\left(3,5\right)$ and $\left(5,13\right)$:

As mentioned earlier, the main error is in:

Also observe that these $n$ number of line segments also divide $OB$ into equal lengths, each equal to $OF$.

Indeed, the calculations are correct until:

the $n$ number of projections also divide $OB$ into equal lengths of $OF$.

This means that $n\ne\dfrac{OB}{OF}$, which poisons the calculations that follow.

Fixing the error

Our two examples above suggest that, rather than $n=\dfrac{OB}{OF}$, we have $\dfrac{OB}{OF}\approx\dfrac{3}{0.33}\approx9$ for $b=3$ and $n=5$, and $\dfrac{OB}{OF}\approx\dfrac{5}{0.2}\approx25$ for $b=5$ and $n=13$. These might lead one to conjecture that $\dfrac{OB}{OF}=b^{2}=2n-1$.

Since $\angle OAF=\angle CAE=\angle ABO$, we have similar right triangles, and $\dfrac{OF}{AO}=\dfrac{AO}{OB}$ so that $OF=\dfrac{1}{b}$. From this, we do indeed have $\dfrac{OB}{OF}=\dfrac{b}{\frac{1}{b}}=b^{2}=2n-1$.

Since $n=\dfrac{H^2}{2}$, we have $\dfrac{OB}{OF}=H^2-1$, which is perfectly consistent with $H^2 = 4a^2 + 8a + 5$ and $\dfrac{OB}{OF} = \dfrac{2a + 2}{1/(2a + 2)} = (2a + 2)^2$ derived in the OP. Unfortunately, this doesn't tell us anything about $a$ (or $b$ or $n$).

Answer 2

First, of course, you have a hand-wavy way of dealing with infinities that makes the entire enterprise suspect. But we can address this by taking $B$ to be a point at a finite distance along the $x$ axis so that we have an actual Euclidean triangle $\triangle AOB.$

So let $B$ have coordinates $(2a + 2, 0)$ as shown below.

The graph of $e^{-x}$ intersects the line $AB$ at two places: $A$ and a point strictly between $A$ and $B.$ If $a$ is large enough, the second intersection will be much closer to $B$ than to $A$ and the graph of $e^{-x}$ will divide the triangle $\triangle AOB$ into two regions, one of which has area $1 - \varepsilon$ and the other of which has area $a + \varepsilon$ for some positive number $\varepsilon.$ As we increase $a$ toward infinity, $\varepsilon$ approaches zero.

So that's how we might deal with your infinity problem. But you have a more elementary error in your calculations: you claim that

$$ \frac{OB}{OF} \stackrel?= \frac{CB}{CE}. $$

But actually triangles $\triangle BFE$ and $\triangle BOD$ in the figure are similar, leading to the conclusion that $$ \frac{OB}{OF} = \frac{DB}{DE}. $$

In fact, $CD = DE = \frac12 CE$ and therefore

$$ \frac{CB}{CE} = \frac{DB}{2 DE} + \frac{CD}{2CD} = \frac12(2a + 2)^2 + \frac12 = 2 a^2 + 4 a + \frac52. $$

Then since $\frac{CB}{CE} = \frac12 H^2$ and $H^2 = 4a^2 + 8a + 5,$ we have $$ 2 a^2 + 4 a + \frac52 = \frac12 (4a^2 + 8a + 5), $$

which of course is true for any $a.$

Answer 3

I did not follow your steps, but the divergent integral $\int_0^\infty 1 dx$ has hegularized value of $0$.

If we subtract the both integrals, the integral $\int_0^\infty (1-e^{-x})dx$, as can be computed by Mathematica using the formula Limit[Sum[s f[x s], {x, 0, ∞}, Regularization -> Dirichlet], s -> 0] /. f[x_] -> (1 - Exp[-x]), has the regularized value of $-1$.

A negative value but not what you got.

Notice though that infinite shapes can have the value of integral over them depending on along which axis you integrate, shift and rotation. So, the divergent integral is not the "area" of the shape as it changes under shift (for instance, along the $x$ axis).