4

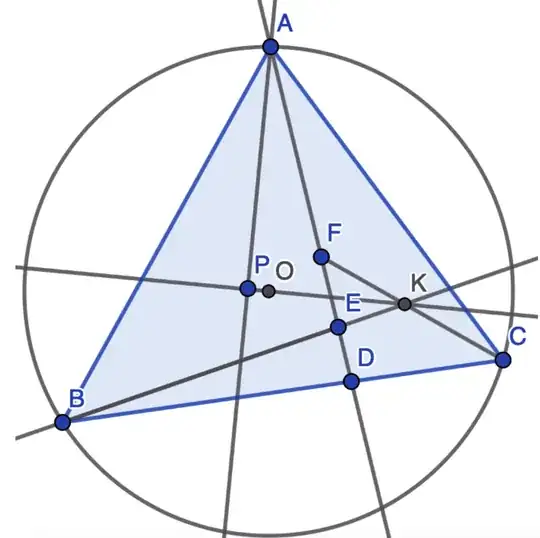
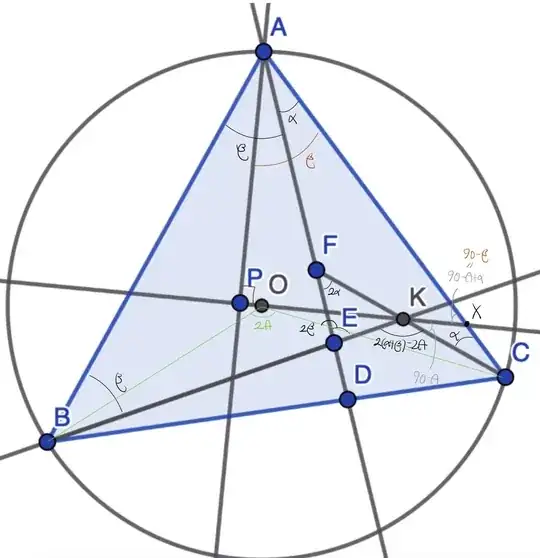
In triangle $\triangle ABC$, let $O$ be the circumcenter, and let $D$ be a point on $BC$. Points $E$ and $F$ lie on the line $AD$ such that $AE=BE$ and $AF=CF$. The lines $BE$ and $CF$ intersect at $K$. Draw $AP$ perpendicular to $OK$ at $P$.

Prove that $\angle BAD = \angle CAP$.

Note that $AE = BE$, $E$ lies on the perpendicular bisector of $AB$ and similarly, $F$ lies on the perpendicular bisector of $AC$. It's also possible that $AP$ and $AD$ are symmetric with respect to the angle bisector of $\angle BAC$. The only way I know to continue is to set coordinates.

Can anyone provide a different solution asap?

Thank you in advance

enter image description here

John O'neil
  • 827
  • 1
    Note that$$\angle BKC=\angle ABK+\angle ACK+A\=\angle BAE+\angle CAF+A=2A=\angle BOC,$$so $B$, $K$, $O$, $C$ are concyclic. The rest is simple angle chasing. – youthdoo Jun 19 '25 at 11:19

3 Answers3

1

enter image description here

In the picture AQ is the bisector of angle BAC. In triangle SAT, AP is the altitude and AQ is the bisector of angle SAT.AZ is the diameter of the circumcircle $d_1$ of the triangle SAT. We use this fact that the bisector of angle SAT is also the bisector of the angle between the altitude and the diameter of the circumcircle , so we have:

$\angle NAQ=\angle QAI$

$\angle BAQ=\angle QAC$

which results in:

$\angle BAN=\angle CAI$

Therefore:

$(\angle CAI+\angle IAN=\angle CAP)=(\angle BAN+\angle NAI=\angle BAD)$

sirous
  • 12,694
  • A shortcut in your solution (+1) — $AP$ is the altitude and $AZ$ is a diameter, so we can use the isogonal conjugate here; orthocenter and circumcenter of SAT are isogonal conjugate, so $AP$ and $AZ$ are isogonal on $\angle A$. – RDK Jun 19 '25 at 13:55
0

My solution is based upon angle chasing, even though it may be a bit of unnecessary bashing. Probably someone will find a better solution to this problem...

Firstly, as usual triangle notation, let $\alpha=\angle BAC$, $\beta=\angle ABC$, $\gamma=\angle BCA$. I will also call $M,N$ the midpoints of $AB,AC$, $\theta=\angle BAD$ and $\phi= \angle DAC=\alpha-\theta$. Then observe that

  1. $\angle EBA=\theta, \angle FCA=\phi$ for basic isosceles triangles properties.
  2. The quadrilateral $BCOK$ is cyclic. It suffices to see that $\angle KBC=\beta-\theta$, $\angle KCB=\gamma-\phi$, and then from triangle sum we have $\angle BKC=2\alpha$. Which is the same as $\angle BOC$, since it has the vertex in the center of $(ABC)$.
  3. Point (2) means that $\angle KOC=\angle KCB=\gamma-\phi$.
  4. Since $\angle MOB=\gamma$, then $\angle MOK=\phi$.
  5. Now $APON$ is cyclic since it has two opposite right angles. $\angle KON=\angle KOM+\angle MOA+\angle AON=\phi+\beta+\gamma$.
  6. Finally $\angle CAP=180^\circ-\angle KON=\theta=\angle BAD$. QED
Isaak09
  • 86
0

Here is my simple solution, which uses only two more construction lines.

enter image description here

  1. Let $\angle A = \alpha + \beta$.

  2. By definition, $\angle ACF = \alpha, \angle ABE = \beta$.

  3. So we get $\angle EFK = 2\alpha, \angle FEK = 2\beta$.

  4. Thus, $\angle BKC = 2(\alpha + \beta) = 2\angle A$.

  5. So we get $(OBCK)$ concyclic.

  6. Using this, we get $\angle XKC = \angle OBC = \frac{\pi}2 - \angle A$.

  7. Using $\angle ACF = \alpha$, we get $\angle AXP = \frac{\pi}2 - \angle A + \alpha = \frac{\pi}2 - \beta$.

  8. Finally, using $\angle APX = \frac{\pi}2$, we get $\angle CAP = \beta = \angle BAD. \blacksquare$

RDK
  • 3,389