7

I was playing with an approximation I found in this question: $$\ln(1+e^x) \approx \begin{cases} \frac{x}{1-e^{-\frac{x}{\ln(2)}}},\quad x\neq 0\\ \ln(2),\quad x=0\end{cases}$$

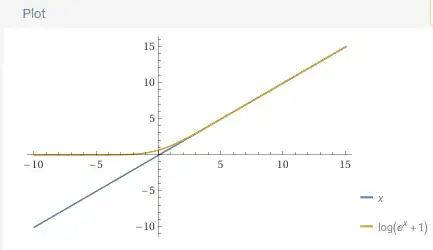
When comparing $f(x) = \ln(1+e^x)$ with $g(x) = x$ you could see that $f(x)$ behaves as a smooth transition from zero to the straight line $g(x)$ as depicted in the plot below by Wolfram-Alpha:

First comparison

So then I tried to integrate them and see how close their integrals are, which intuition says should approximate a quadratic function $G_{q}(x) = \frac{x^2}{2}$. By taking the integral in Wolfram-Alpha shows it matches $$F(x) = \int\ln(1+e^x)dx = -\text{Li}_2(-e^x)$$ with $\text{Li}_n(x)$ the Polylogarithm function with parameter $n=2$ (later through the answers I realized the function is named Dilogarithm).

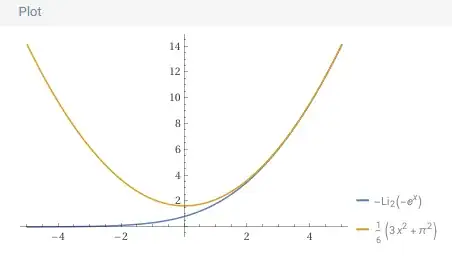
When comparing the plots of $F(x)$ with the quadratic $G_q(x)$ I noticed that for big values of $x$ there was always an offset difference, so I took the limit of the difference in Wolfram-Alpha and result it was coincidentally the result of the Basel problem: $$\lim\limits_{x\to\infty} \left[-\text{Li}_2(-e^x)-\frac{x^2}{2}\right] = \frac{\pi^2}{6}$$

and indeed by using $G(x)=\frac{x^2}{2} + \frac{\pi^2}{6}$ the function matches $F(x)$ for big values of $x$ as one could see in Wolfram-Alpha:

Second comparison

With this I found an smooth transition function between zero and a quadratic function through $F(x)$.

But now, my question is: Is this just a coincidence? Or there is a relation to the Basil problem I cannot see?

Added later

Furthermore, $$\int\limits_{-\infty}^0 2\ln(1+e^x)\ dx = \frac{\pi^2}{6}$$

As also by the approximation, $$\int\limits_{-\infty}^0 \dfrac{x}{\ln^2(2)(1-e^{-\frac{x}{\ln(2)}})}\ dx = \frac{\pi^2}{6}$$

And, $$\int\limits_{-\infty}^0 \dfrac{x}{(1-e^{-x})}\ dx = \frac{\pi^2}{6}$$

All of them associated to $\operatorname{Li}_2(e^x)$ or $\operatorname{Li}_2(-e^x)$.

Joako
  • 1,957

1 Answers1

10

Wikipedia lists an identity$\DeclareMathOperator{\Li}{Li}$ $$\Li_2(z)+\Li_2\left(\frac1z\right)=-\frac{\pi^2}{6}-\frac{\ln(-z)^2}{2}$$ With that identity, one sees $$\Li_2(-e^x)=\Li_2(-e^{-x})-\frac{\pi^2}{6}-\frac{x^2}{2}$$ With the fact that $\Li_2(0)=0$, one recovers the said identity.

Why does $\pi^2/6$ pop up here? That is very natural: $$\Li_2(1)=-\int_0^1\frac{\ln(1-t)}{t}\,\mathrm dt=\sum_{k=1}^{\infty}\frac1{k^2}=\frac{\pi^2}{6}$$ This is a very standard thing about dilogarithm, which you can find anywhere. In fact, one can even define it that way: $$\Li_2(z)=\sum_{k=1}^{\infty}\frac{z^k}{k^2}$$ for $|z|\le1$, and the analytic continuation elsewhere.

For a proof of the identity at the beginning, see this.

Hope this helps. :>

ultralegend5385
  • 10,106
  • Nice answer... I was not aware about these relations between logarithms and $\pi$ – Joako Jun 18 '25 at 03:14
  • It is interesting, I still don't get how the functions are related to circles (given $\pi$), but $\int_0^1 \frac{-\ln(1-t)}{t}\ dt = \frac{\pi^2}{6}$ as you mentioned, but also $\int_{-1}^0 \frac{-\ln(1-t)}{t}\ dt = \frac{\pi^2}{12}$ so you get $\int_{-1}^1 \frac{-\ln(1-t)}{t}\ dt = \frac{\pi^2}{4}$ – Joako Jun 18 '25 at 15:35
  • 1
    @Joako: There is a marvelous video of 3b1b for that. – ultralegend5385 Jun 18 '25 at 17:02
  • Nice... I think I saw it before, what it is not shown is the relation with the logarithm... exponentials and circles are quite related by Euler's Identity, but I was not expecting to found also a relation between circles and logarithms – Joako Jun 18 '25 at 18:41
  • Particularly, $$\int\limits_{-\infty}^0 \ln(1+e^x)\ dx=\frac{\pi^2}{12}$$ – Joako Jun 18 '25 at 18:48
  • 1
    @Joako: I don't know of any "natural" way to see it but from the Taylor series$$\frac{\ln(1-t)}{t}=\sum_{n=1}^{\infty}\frac{t^{n-1}}{n}$$it doesn't look too surprising. – ultralegend5385 Jun 19 '25 at 03:06
  • I accidentally found today a YT short explaining the relation. – Joako Jun 20 '25 at 19:56