2

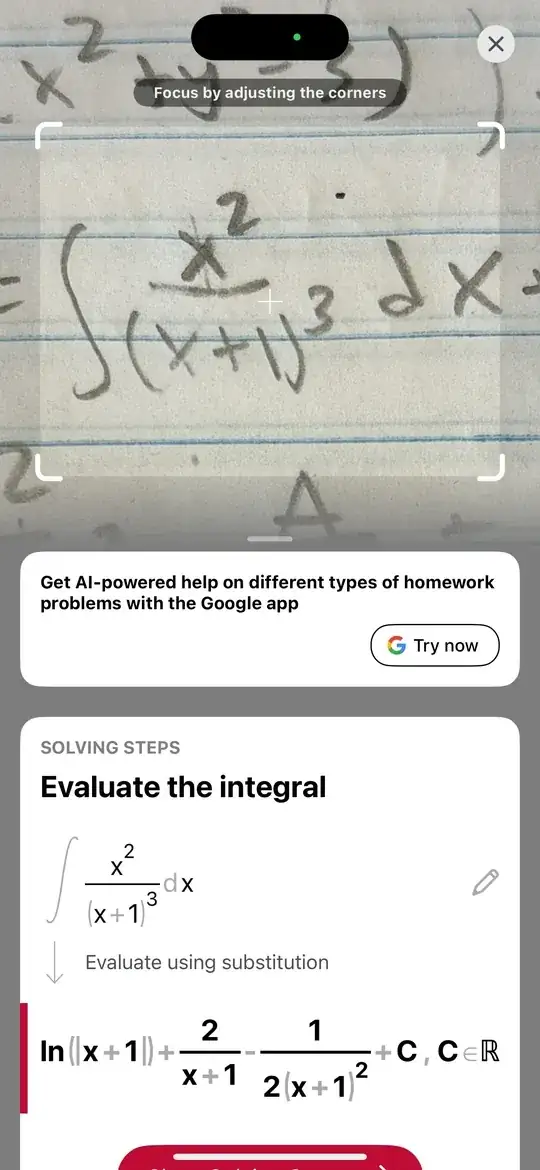
I had the integral $\frac{x^2}{(x+1)^3}$, partial fraction decomposition gave $\frac{1}{x+1} -\frac{2}{(x+1)^2} + \frac{1}{(x+1)^3}$, and so the solution was $\ln|x+1| + \frac{2}{x+1} - \frac{1}{2(x+1)^2} + C$, but the calculator said it was that solution but added $-\frac{1}{2}$ to the end. Did it calculate the $+ C$ or something?

Here are some pictures of what I inputted into the calculator, and its solution expanded. And there is a picture of photomath saying the original solution without the $\frac{1}{2}$ was correct. Thank you. enter image description here

1st part of expanded solution 2nd part of expanded solution photomath solution/what i got

CiaPan
  • 13,884
karimelg
  • 21
  • 3
  • 9
    There is no difference between an unknown additive constant $C$ and the term $C-\frac 12$. That is to say, the $-\frac 12$ can simply be absorbed into the constant. – lulu Jun 17 '25 at 18:41
  • 1
    https://math.stackexchange.com/q/3453558/42969 – Martin R Jun 17 '25 at 18:51
  • A constant minus a number is still a constant. – Sean Roberson Jun 17 '25 at 18:52
  • oh i get it know, thank you. So when i go to check my integral should I always expand it to then remove that constant so i dont mess up or it doesnt matter. – karimelg Jun 17 '25 at 18:58
  • It looks like the integral is being calculated by calculating: $$\int_0^x f(t),dt$$ Maybe the calculator always does this? – Thomas Andrews Jun 17 '25 at 20:22
  • The specific constant only matters for definite integral. The constant doesn't matter for checking the answer, since the derivative of a constant is zero, but the calculator should add back in the constant variable, since the indefinite integral yield not one function, but a class of functions. – Thomas Andrews Jun 17 '25 at 20:24

2 Answers2

1

The $+C$ is an arbitrary constant that arises from the antiderivative, (See Matrin R's link for more info,) so there is no way to "calculate the $+C$". Constant terms that are added to the solution can simply be absorbed to the $+C$ term to improve clarity.

Mattan Feldman
  • 324
1

\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}\left(\ln |x+1|-\frac{x^2-2x-2}{2(x+1)^2}\right) =\frac{1}{1+x}-\frac{2x+1}{(x+1)^3}&=\frac{(x+1)^2-2x-1}{(x+1)^3} \\ &=\frac{x^2}{(x+1)^3} \end{aligned}

So technically, the answer is the same, and the comment by Thomas Andrews still stands there's a class of function so you can add anything like for example take this integrand $\int \frac{1}{(1-x)^2}\mathrm{d}x$ The answer for it is $\frac{1}{1-x}+C$ but also it's can be $\frac{x}{1-x}$ if we add -1+1 and the one plus C becomes a new constant.

StarKiller
  • 11
  • 1