Asymptotics of constrained multinomial coefficients

Question

Given 4 non-negative integers $n_1,n_2,n_1^\prime,n_2^\prime$ so that $n_1+n_2=n_1^\prime+n_2^\prime=N$, I have the multinomial coefficient $$ \binom{N}{t_1, t_2, t_3, t_4} $$ where $$ t_1+t_3=n_1\, ,\quad t_2+t_4=n_2\, ,\quad t_1+t_2=n_1^\prime\, , \quad t_3+t_4=n_2^\prime. $$ One can then solve $$ t_2=n_1^\prime-t_1\ge 0\, ,\quad t_3=n_1-t_1\ge 0\, ,\quad t_4=n_2^\prime-n_1+t_1\ge 0 $$ which restricts the values of $t_1$, and expresses all the $t_k$ in terms of $t_1$ and the known $n$'s and $n^\prime$'s. The value of the multinomial coefficient as a function of $t_1$ is then "almost" Gaussian.

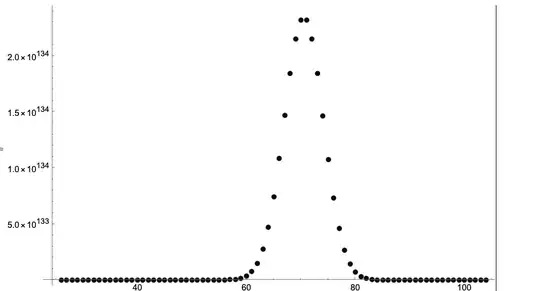
For instance, with $$ N=242\, , n_1=164\, ,n_2=78\, , n_1^\prime =104\, ,n_2^\prime=138\, , $$ we have the following:

where the horizontal axis is $t_1$ and the vertical the value of the multinomial coefficient. The maximum is located at $T_1=71$, although $t_1=70$ is actually numerically very close to the maximum. Without proof, I found this value of $T_1$ to be almost $n_1\times n_1^\prime/N\approx 70.47$ : I can just take the integer part of $n_1\times n_1^\prime/N$ for a very good estimate of this $T_1$, a very convenient expression in terms of the initial data $n_k,n_k^\prime$.

I know from here that $$ \binom{n}{a_1,\ldots,a_k} \sim(2\pi n)^{1/2-k/2}k^{n+k/2}\exp\Big\{-\frac k{2n}\,\sum_{i=1}^k(a_i-n/k)^2\Big\} \tag{1} $$ so subbing $a_i\mapsto t_i$ I obtain (with $k=4$ and $n\mapsto N=242$) $$ \sum_{i=1}^k(a_i-n/k)^2=23747-588 t_1+4t_1^2\\ =4\left(t_1-\frac{147}{2}\right)^2+2138\, . $$ The min of this is reached at $t_1=\frac{147}{2}= 73.5$, which is "not that far" from my guess $n_1\times n_1^\prime/N \approx 70.47$.

Taking various other combinations of $(n_1,n_2,n_1^\prime,n_2^\prime)$ indicates that $n_1 n_1^\prime/N$ is always a better approximation to the location of $T_1$ than starting with Eq.(1). The product $n_1 n_1^\prime /N$ is related to products of Gaussians as per this post

Is there a way to prove the guess $n_1\times n_1^\prime/N$ for the approximate value of $t_1$ that produces the maximum, and is there a systematic way to approximate location of the maximum and the "width" of the Gaussian-like curve in general (for larger $k$) given the initial data, and in particular do so when the $t_i$'s are not independent as in the example given above?

Answer 1

I think that large deviations would be more appropriate in your case. It is valid when scales as $t=N\tau$ and $n=N\nu$. Physically, $t,n$ are extensive, while $\tau,\nu$ are the corresponding intensive variables.

The multinomial is therefore: $$ \binom N{t_1,t_2,t_3,t_4}\asymp\exp\left[-N\left(\sum_{i=1}^4\tau_i\ln\tau_i\right)\right] $$ under the constraint: $$ \tau_1+\tau_3=\nu_1 \quad \tau_2+\tau_4=\nu_2 \\ \tau_1+\tau_2=\nu_1' \quad \tau_3+\tau_4=\nu_2'\\ \nu_1+\nu_2=\nu_1'+\nu_2'=1 $$ You can now maximize entropy: \begin{align} S&= -\tau_1\ln\tau_1 -(\nu_1'-\tau_1)\ln(\nu_1'-\tau_1)\\ &\quad -(\nu_1-\tau_1)\ln(\nu_1-\tau_1)-(\nu_2'-\nu_1+\tau_1)\ln(\nu_2'-\nu_1+\tau_1)\\ \frac{dS}{d\tau_1}&=\ln\left(\frac{(\nu_1-\tau_1)(\nu_1'-\tau_1)}{\tau_1(\nu_2'-\nu_1+\tau_1)}\right) \end{align} so you find by setting $\frac{dS}{d\tau_1}=0$: $$ \tau_1=\nu_1\nu_1'\\ t_1=\frac{n_1n_1'}N $$

As usual, you can also recover a central limit theorem by Taylor expanding about the maximum. The variance (heat capacity/susceptibility for physicists) is: $$ \frac{d^2S}{d\tau_1^2}=-\frac1{\nu_1-\tau_1}-\frac1{\nu_1'-\tau_1}-\frac1\tau_1-\frac1{\nu_2'-\nu_1+\tau_1} \\ =-\frac1{\nu_1\nu_2'}-\frac1{\nu_1'\nu_2}-\frac1{\nu_1\nu_1'}-\frac1{\nu_2\nu_2'} $$ so the variance of $t_1$ is: $$ \Delta t_1^2=\frac1{\frac N{n_1n_2'}+\frac N{n_1'n_2}+\frac N{n_1n_1'}+\frac N{n_2n_2'}} $$

Hope this helps.