2

In Mario Party, there exists two items (Double Dice, Mushroom), and I'm interested in seeing which is better probabilistically.

  1. Double Dice (X). Roll two dice, each ranging 1-10, then compute it's sum.
  2. Mushroom (Y). Roll one dice, ranging 1-10, then add +5 to the roll.

I'm looking for when: $P(X>Y)$, i.e, what is the probability that you will roll more with double dice v.s. mushroom. A general approach for when $P(X>Y)$ for any two discrete random variables would be appreciated as well. I found on other posts that this is equivalent to when $P(X-Y>0)$, but I'm not necessarily sure how to compute this quantity when X and Y are not normal distributions.

I've graphed the distributions for $X$ and $Y$ below for reference (note the scaling!)

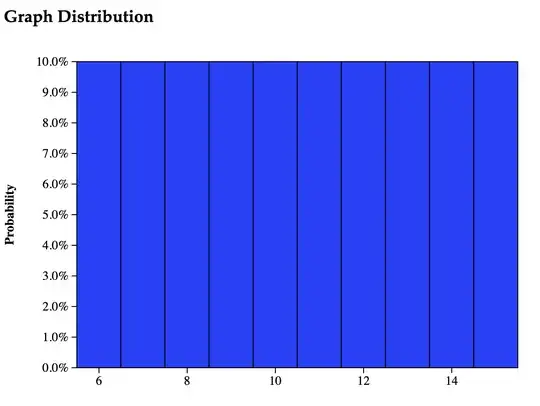Double Dice Mushroom I don't have much experience with probability besides an introductory calculus based statistics course a few years ago, so any explanation will go a long way. Also, if there are names for these distributions and the distribution of $X-Y$, that would be appreciated as well.

EDIT: My first idea in computing $P(X>Y)$ is to compute $$\sum_{k=2}^{20} P(X>k)$$ i.e, fixing $Y$ and adding up all the probabilities that $X$ is greater than some value of $k$. But I don't think this gives a valid probability distribution (sum is > 1) and am curious why this approach doesn't work.

Davide Giraudo
  • 181,608
Conrad12345
  • 112

1 Answers1

2

It turns out that $$ P(X>Y)=1/2. $$

Let $D_1,D_2,D_3$ denote three 10-sided die rolls. Letting $X=D_1+D_2$ and $Y=D_3+5$, we seek $$ P(X>Y)=P(D_1+D_2>D_3+5) $$ The clever trick is to notice that $D_3$ is symmetrically distributed on the range $\{1,2,\dots,10\}$, so that $11-D_3$ has the same distribution as $D_3$. Therefore, we can replace $D_3$ with $11-D_3$ above, leading to the equivalent probability $$ P(X>Y)=P(D_1+D_2>(11-D_3)+5)=P(D_1+D_2+D_3>16). $$ Note that the expected value of $D_1+D_2+D_3$ is equal to $5.5\times 3=16.5$, so we are asking for the probability that $D_1+D_2+D_3$ is greater than its mean. But the sum $D_1+D_2+D_3$ is symmetrically distributed over the range $\{3,\dots,30\}$, so it is equally likely to be greater than its mean as it is to be less than its mean. Therefore, we get $P(X>Y)=1/2$, as claimed.

We can also work out the value of $P(X<Y)$. This is just $$ P(X<Y)=1-P(X>Y)-P(X=Y)=1/2-P(X=Y). $$ We can work out $P(X=Y)$ using a similar trick: $$ P(X=Y)=P(D_1+D_2+D_3=16). $$ We need the probability that the sum of three 10-sdied dice sum to 16. Using the well-known formula for the probability that several $10$-sided dice sum to a number, this probability is $$ 10^{-3}\left(\binom{15}2-3\binom{5}2\right)=0.075. $$ In conclusion, we have $$ P(X>Y)=50\%, \qquad P(X=Y)=7.5\%, \qquad P(X<Y)=42.5\%, $$ so the double dice is better a little more often than the mushroom.

Mike Earnest
  • 84,902