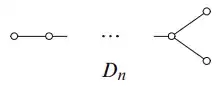1

Consider the $\mathfrak{so}_{2n}$ Lie algebra over $\mathbb{C}$, $n\geq 2$. Consider $U=\mathbb{R}^n$, and a basis of $U$ given by the roots

\begin{equation} e_1-e_2,e_2-e_3,\ldots,e_{n-2}-e_{n-1},e_{n-1}-e_n,e_{n+1}+e_n. \end{equation}

See Brian C. Hall, Lie groups, Lie algebras, and representations. An elementary introduction, Graduate Texts in Mathematics 222, Cham: Springer, pp. xiii+449 (2015), MR3331229, Zbl 1316.22001, page 240 for more details. The associated Dykin diagram is

                                                        

However, I struggle to understand how the last vertex with an angle arise. The rule I use to construct a Dynkin diagram (see definition $8.31$ in Lie Groups, Lie Algebras, and Representation) do not describe the construction of such diagrams, but it seems to me they would only describe diagrams with vertices on a straight line, such as the one for $A_n$, $B_n$ or $C_n$.

Daniele Tampieri
  • 10,752
QuantizedObject
  • 333
  • 2
    Take $D_4$ first to see this, with the Cartan numbers. Then you see, it is not $A_4$. – Dietrich Burde May 26 '25 at 10:19
  • If you want to see how the root spaces are located in the algebra, then may be take a look at this recent answer of mine. That is for $\mathfrak{o}(8)$ only, but the placement is easy to guess after having seen that. A caveat I need to make is that I used the variant of the matrix algebram where the preserved quadratic form look like $$x_1x_{2n}+x_2x_{2n-1}+\cdots+x_nx_{n+1}.$$ It is easy to check that this is similar to the more common sum of squares. – Jyrki Lahtonen May 28 '25 at 12:39
  • (cont'd) The variant is motivated by the nice properties that A) a maximal torus consists of diagonal matrices within the algebra, and B) the positive root spaces correspond to upper triangular matrices. – Jyrki Lahtonen May 28 '25 at 12:40
  • 1
    The more natural version of the Lie algebra makes the maxima torus as well as the root algebras look a bit unwieldy. At least in comparison to the test case of $\mathfrak{sl}_n$. – Jyrki Lahtonen May 28 '25 at 12:51

1 Answers1

4

Recall given a base $\Delta=\{\alpha_1,\dots,\alpha_r\}$ of a rank-$r$ root system, the associated Dynkin diagram is obtained by following the rules:

  1. The Dynkin diagram is a graph with vertices $v_1,\dots,v_r$ corresponding to each element $\alpha_i \in\Delta$.
  2. Between any two vertices $v_i$ and $v_j$, place $0,1,2,$ or $3$ edges depending on whether the angle between $\alpha_i$ and $\alpha_j$ is $\frac{\pi}{2},\frac{2\pi}{3},\frac{3\pi}{4}$, or $\frac{5\pi}{6}$.
  3. Arrows point from the longer root to the shorter root.

In the case of $D_n$, as you claim correctly, a base is given by $\Delta=\{e_1-e_2,e_2-e_3,\dots,e_{n-2}-e_{n-1},e_{n-1}-e_n,e_{n-1}+e_n\}$. These all have the same length, so no arrows needed. You may check that except for the last element, any two consecutive roots in that list have an angle $\frac{2\pi}{3}$, and any non-consecutive roots are orthogonal. This gives us the first $n-1$ vertices in a line. Lastly, note that the root $e_{n-1}+e_n$ forms an angle $\frac{2\pi}{3}$ with the second-last $e_{n-1}-e_n$ and is orthogonal to every other root. This is why the Dynkin diagram of $D_n$ looks as you have shown.

Landuros
  • 3,030