1

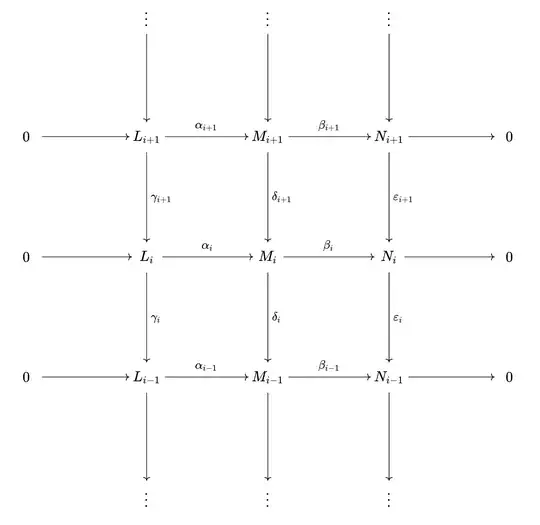
The statement of the problem (Aluffi III.7.17) is as follows:

Consider a (possibly infinite) commutative diagram of $R$-modules in which the central column is a complex and every row is exact. Prove that the left and right columns are also complexes. Prove that if any two of the columns are exact, so is the third.

enter image description here

I have no problem proving the first statement, it is the second in bold that is causing me some difficulty. What remains is showing 3 cases. Here is what I have attempted so far:

Case 1: If column 1 and 2 are exact then column 3 is exact. Need to show $\ker\varepsilon_i\subseteq\text{im }\varepsilon_{i+1}$.

Let $n_i\in\ker\varepsilon_i$. Then $\varepsilon_i(n_i)=0$. Since $\beta_i$ is surjective $\exists m_i\in M_i$ such that $\beta_i(m_i)=n_i$. So $\varepsilon_i\circ\beta_i(m_i)=0$. By commutativity of the diagram, $\beta_{i-1}\circ\delta_i(m_i)=0$. Then $\delta_i(m_i)\in\ker\beta_{i-1}=\text{im }\alpha_{i-1}$ so $\exists l_{i-1}\in L_{i-1}$ such that $\alpha_{i-1}(l_{i-1})=\delta(m_i)$. (Not sure where to go from here, I suspect injectivity of $\alpha_{i-1}$ may need to be used but I’m not exactly sure how).

Case 2: If column 1 and 3 are exact then column 2 is exact. Need to show $\ker\delta_i\subseteq\text{im }\delta_{i+1}$.

Let $m_i\in\ker\delta_i$. Then $\delta_i(m_i) = 0$ and thus $\beta_{i-1}\circ\delta_i(m_i)=0$. By commutativity of the diagram, $\varepsilon_i\circ\beta_i(m_i)=0$. Then $\beta_i(m_i)\in\ker\varepsilon_i=\text{im }\varepsilon_{i+1}$. So $\exists n_{i+1}\in N_{i+1}$ such that $\varepsilon_{i+1}(n_{i+1}) = \beta_i(m_i)$. $\beta_{i+1}$ is surjective so $\exists m_{i+1}\in M_{i+1}$ such that $\beta_{i+1}(m_{i+1})=n_{i+1}$. So $\varepsilon_{i+1}\circ\beta_{i+1}(m_{i+1})=\beta_i(m_i)$. By commutativity of the diagram once more, $\beta_i\circ\delta_{i+1}(m_{i+1})=\beta_i(m_i)$. So $\beta_i(\delta_{i+1}(m_{i+1})-m_i)=0$. Then $\delta_{i+1}(m_{i+1})-m_i\in\text{im }(\alpha_i)$ so $\exists l_i\in L_i$ such that $\alpha_i(l_i)=\delta_{i+1}(m_{i+1})-m_i$. Separately, $\delta_i\circ\alpha_i(l_i)=\alpha_{i-1}\circ\gamma_i(l_i)$ and thus $\gamma_i(l_i)=0$. So $l_i\in \text{im }\gamma_{i+1}$ so $\exists l_{i+1}\in L_{i+1}$ such that $\gamma_{i+1}(l_{i+1})=l_i$. So $\alpha_i\circ\gamma_{i+1}(l_{i+1})=\delta_{i+1}(m_{i+1})-m_i$ and by commutativity it follows that $\delta_{i+1}(m_{i+1}-\alpha_{i+1}(l_{i+1}))=m_i$, i.e. $\ker\delta_i\subseteq\text{im }\delta_{i+1}$.

Case 3: If column 2 and 3 are exact then column 1 is exact. Need to show $\ker\gamma_i\subseteq\text{im }\gamma_{i+1}$.

Let $l_i\in\ker\gamma_i$. Then $\gamma_i(l_i)=0$ so $\alpha_{i-1}\circ\gamma_i(l_i) = 0$. Then $\delta_i\circ\alpha_i(l_i)=0$. By exactness of the middle column there exists $m_{i+1}\in M_{i+1}$ such that $\delta_{i+1}(m_{i+1})=\alpha_i(l_i)$. (Similarly to case 1 I get stuck here and suspect I need to use injectivity of $\alpha_i$).

Any pointers in the right direction would be very much appreciated. Thanks in advance!

iceberg56
  • 73
  • 1
    Search for the ninr lemma or 3x3 lemma. This is almost certainly a duplicate. – Lukas Heger May 25 '25 at 21:59
  • @LukasHeger nine lemma seems to require top / bottom rows being all zeroes which is not the case here – iceberg56 May 25 '25 at 22:08
  • 1
    I don't have Aluffi at hand, but does he cover the long exact sequence in cohomology induced by a short exact sequence of complexes? If you apply this, it's pretty straightforward. A complex is exact iff it has zero cohomology. – Lukas Heger May 25 '25 at 22:12
  • @LukasHeger he does make a comment to this effect: The first part is straightforward. The second part will take you a couple of minutes now due to the needed diagram chases, and a couple of seconds later, once you learn about the long exact (co)homology sequence in §IX.3.3. Since this is in a very introductory section to homology where we really only have the snake lemma I would like to try and prove the two cases with a diagram chase instead of resorting to the more advanced methods that will show up later in the book – iceberg56 May 25 '25 at 22:17
  • Usually this exercise is with zero rows on top and bottom, see here. Then the Snake Lemma resp. Salamander Lemma can be used. But diagram chasing also works. I suppose you have now enough ideas to proceed. – Dietrich Burde May 26 '25 at 09:18
  • @DietrichBurde do you have any advice on how I might be able to proceed with a diagram chase given the work I have shown above? – iceberg56 May 26 '25 at 17:37

1 Answers1

1

The question in case 1: Let $m_{i-1}$ denote $\delta_i (m_i)$. Note that, because the central column is a complex, $\delta_{i-1}(m_{i-1}) =0$. By commutativity this means that $\alpha_{i-2}(\gamma_{i-1}(l_{i-1}) =0 $, and because this map is injective we conclude that $\gamma_{i-1}(l_{i-1}) = 0$. Thus it lifts to some $l_{i}$, now consider $m_i - \alpha_i(l_i)$. On the one hand this maps to the original $n_i$ through $\beta_i$, and on the other hand it is mapped to $0$ by $\delta_i$. Hence it lifts to some $m_{i+1}$ and $\beta_{i+1}(m_{i+1})$ is your desired lift.

The question in case 3: Let $m_i$ denote $\alpha_i(l_i)$. As you mentioned this lifts to some $m_{i+1}$. Let $n_{i+1}$ denote $\beta_{i+1}(m_{i+1})$. Observe that, $\varepsilon_{i+1}(n_{i+1})=0$ because $\beta_i(m_i)=0$, hence $n_{i+1}$ lifts to some $n_{i+2}$. By exactness of the rows there is some $m_{i+2}$ such that $\beta_{i+2}(m_{i+2})=n_{i+2}$. Consider $m_{i+1} - \delta_{i+2}(m_{i+2})$. On the one hand this maps to $0$ through $\beta_{i+1}$, and on the other hand it is mapped to $m_i$ by $\delta_{i+1}$. Now, by exactness of the $(i+1)$'th row there is some $l_{i+1}\in L_{i+1}$ such that $\alpha_{i+1}(l_{i+1}) = m_{i+1} - \delta_{i+2}(m_{i+2})$. This is the desired lift of $l_i$ because $\gamma_{i+1}(l_{i+1}) - l_i$ gets mapped to $0$ by $\alpha_i$ because of the commuting square, the claim then follows from the injectivity of $\alpha_i$.

Hidde Bakker
  • 126