Asymptotic Behavior of a Recurrence Sequence

Question

During my studies, I stumbled upon the following recurrence. \begin{align*} a_n = 2 \sum_{k=0}^n \binom{n}{k} \frac{a_k}{2^n}, \qquad n \ge 2, \end{align*} with initial conditions $a_0=a_1=1$.

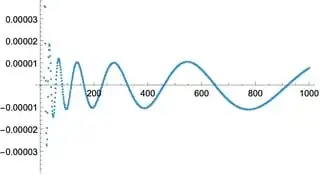
I imagine there is no closed form for this recurrence. However, I am only interested in proving that $$\lim_{n\to\infty} \frac{a_n}{n} = c, $$ where $c>0$ is a constant. Numerically, I found out that $c\approx 1.443$ (using the first 1000 terms).

---

The comic part is that if the initial conditions were $a_0=0$ and $a_1=1$, then the solution would be trivial: $a_n = n$.

---

Furthermore, a strange thing happened when I was determining the exponential generating function $\displaystyle E(z) = \sum_{n=0}^\infty \frac{a_n}{n!}z^n$ of the sequence in terms of $a_0$ and $a_1$. I got $$ 2\,e^z E(z)-E(2 z)= (1+2z)\,a_0,$$ which does not depend on $a_1$. How is this possible?

Answer 1

$\DeclareMathOperator{\EG}{EG}$ $\DeclareMathOperator{\Res}{Res}$ Start with $$b_n=\sum_{k=0}^{n}\binom{n}{k}\frac{a_k}{2^n}=\sum_{k=0}^{n}\binom{n}{k}\frac{a_k}{2^k}\frac{1}{2^{n-k}}=\left(\frac{a_k}{2^k}\circ\frac{1}{2^k}\right)_n$$ $(u_k\circ v_k)$ denotes binomial convolution. We have: $$\left(\sum_{n=0}^{\infty}\frac{a_n}{2^n}\frac{x^n}{n!}\right)\left(\sum_{n=0}^{\infty}\frac{1}{2^n}\frac{x^n}{n!}\right)=\sum_{n=0}^{\infty}b_n\frac{x^n}{n!}=\frac{a_0}{2}(1+x)+\frac{1}{2}\sum_{n=0}^{\infty}a_n\frac{x^n}{n!}$$ $$\iff \EG(a_n;x/2)e^{x/2}=\frac{a_0}{2}(1+x)+\frac{1}{2}\EG(a_n,x)$$ $$\iff 2e^{-x}\EG(a_n;x)-e^{-2x}\EG(a_n;2x)=a_0(1+2x)e^{-2x}$$ Let $F(x)=a_0^{-1}e^{-x}\EG(a_n;x)$ , we have a linear functional equation: $$2F(x)-F(2x)=(1+2x)e^{-2x}$$ The kernel equation $2F(x)-F(2x)=0$ has differentiable (at $0$) solution $F_0(x)=\alpha x$, so we only need to find the particular solution $F_1(x)$. Using Mellin transform: $$\int_{0}^{\infty}(2F(x)-F(2x))x^{s-1}dx=\int_{0}^{\infty}(1+2x)e^{-2x}x^{s-1}dx$$ $$\iff(2-2^{-s})\int_{0}^{\infty}F(x)x^{s-1}dx=2^{-s}(s+1)\Gamma(s)$$ $$\implies F(x)=\frac{1}{2\pi i}\int_{1-i\infty}^{1+i\infty}\frac{(s+1)\Gamma(s)}{2^{s+1}-1}x^{-s}ds$$ To use residue theorem, turn line integral into a box integral vertices($-N+it,1+it,1-it,-N-it$) where you can bound the integral over horizontal edges by $\Gamma(h\pm it)$ (see here) and integral over left edge by gamma reflection formula $\Gamma(-N+it)=\frac{\pi}{\sin(\pi(-N+it))\Gamma(1+N-it)}$ and prove those integrals will eventually vanish, leave us with: $$F(x)=\sum\Res\frac{(s+1)\Gamma(s)}{2^{s+1}-1}x^{-s}$$ The residue where $2^{s+1}-1=0$ contributes to kernel solution so we will ignore them, our poles left are $0,-2,-3,...$. Thus our general solution is $$F(x)=\alpha x+\left(1+\sum_{k=2}^{\infty}\frac{(-1)^k(k-1)}{k!(1-2^{1-k})}x^k\right)$$ Notice that $F(x)=a_0^{-1}e^{-x}\EG(a_n;x)$ so $[x]F(x)=a_0^{-1}a_1-1$, we pick $\alpha=a_0^{-1}a_1-1$ $$\EG(a_n;x)=a_0e^xF(x)\implies a_n=a_0\left(1\circ k![x^k]F(x)\right)$$ $$a_n=(a_1-a_0)n+a_0\left(1+\sum_{k=2}^{n}\binom{n}{k}\frac{(-1)^k(k-1)}{1-2^{1-k}}\right)$$ We are focusing on $c_n=\sum_{k=2}^{n}\binom{n}{k}\frac{(-1)^k(k-1)}{1-2^{1-k}}$ , using geometric expansion: $$c_n=\sum_{k=2}^{n}\binom{n}{k}(-1)^k(k-1)\sum_{j=0}^{\infty}2^{j-jk}$$ $$=\sum_{j=0}^{\infty}2^j\frac{d}{dx}\left(-\frac{1}{x}+n2^{-j}+\sum_{k=0}^{n}\binom{n}{k}(-x2^{-j})^{k}x^{-1}\right)\Big|_{x=1}$$ $$=\sum_{j=0}^{\infty}2^j\frac{d}{dx}\left(-\frac{1}{x}+n2^{-j}+\frac{1}{x}\left(1-x2^{-j}\right)^n\right)\Big|_{x=1}$$ $$=\sum_{j=0}^{\infty}\left(\frac{1-(1-2^{-j})^n}{2^{-j}}-n(1-2^{-j})^{n-1}\right)$$ By Euler-Maclaurin formula: $$c_n\sim\int_{0}^{\infty}\left(\frac{1-(1-2^{-j})^n}{2^{-j}}-n(1-2^{-j})^{n-1}\right)dj$$ $$\overset{t=1-2^{-j}}{=}\frac{1}{\log2}\int_{0}^{1}\frac{1-t^n-nt^{n-1}+nt^n}{(1-t)^2}dt=\frac{1}{\log2}\int_{0}^{1}\sum_{k=0}^{n-1}kx^{k-1}dx=\frac{n}{\log2}$$ Since $a_n=(a_1-a_0)n+a_0(1+c_n)$: $$\lim_{n\to\infty}\frac{a_n}{n}=a_1-a_0+\frac{a_0}{\log2}$$

Answer 2

Empirically, the constant in question seems to be $c = 1/\log2 \approx 1.442695040888963$. More precisely, $\frac{a_n}n - \frac1{\log2}$ seems to act like a function $f(n)/\log n$ with the property that $f(2^m)$ is a periodic function of $m$ with period $1$. Here's a graph of $(\frac{a_n}n - \frac1{\log2} ) \log n$: