How many triangles are in this given figure?

Question

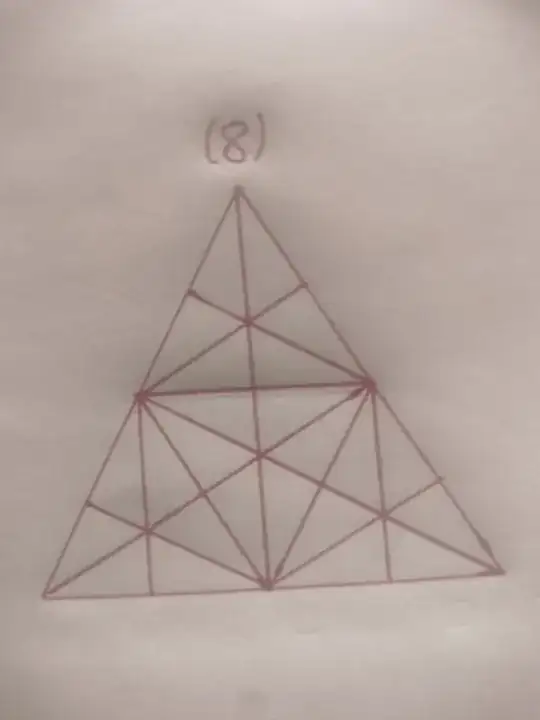
In above problem, there are $104$ triangles. This triangle contains $4$ smaller triangles in which $3$ triangles are at corners and one in the centre of biggest triangle. Each smaller triangle contains $15$ triangles except itself. The big triangle also contains $15$ triangles except itself. So there are $15 \times 5+1$(outermost big triangle)=$76$ triangles. Also this biggest triangle breaks three such triangles: 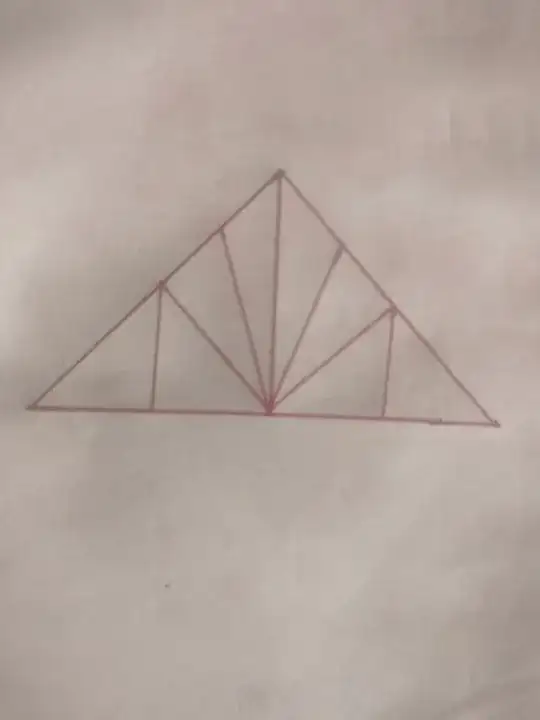. Each such triangles contains 13 triangles. So total triangles = $76+13 \times 3=76+39=115$. Please help me to count triangles on each side of big triangle that not contained in $4$ smaller triangles. I saw this question How many triangles are there? on this website but couldn't understand the concept of $13$ triangles on each side of biggest triangle.

Answer 1

I would count $24$ single little triangles, $12+6$ triangles with two little triangles, $24$ triangles with three little triangles, $12$ triangles with four little triangles, $6+4$ triangles with six little triangles, $3$ triangles with eight little triangles, $6$ triangles with nine little triangles, $6$ triangles with twelve little triangles, $1$ big triangle with twenty-four little triangles.

So $104$ in total.

Here is an illustration: