1

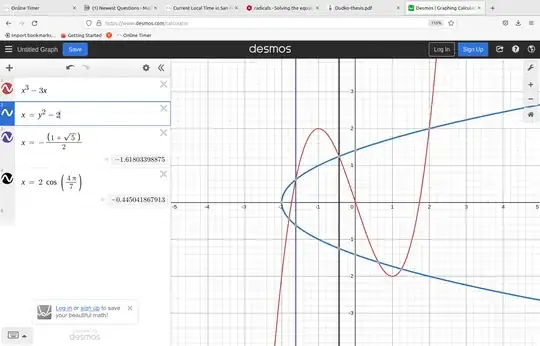
I'm trying to solve the equation

$$x^3 - 3x = \sqrt{x + 2}$$

for $x \in \mathbb{C}$.

The roots of the equation include $x=2$, $x=2\cos4\pi/5$, and $x=2\cos4\pi/7$. However, I want to see how exactly one derives the solution in a rigorous, proof-like way, preferably by myself. I'd like some pointers.

I started by squaring both sides, which gives:

$$(x^3 - 3x)^2 = x + 2$$

Then I let $y = x^2$, and after some manipulation, I ended up with an equation of the form:

$$y(y - 3)^2 = \sqrt{y} + 2$$

But I'm unsure where to go from here, and I feel like I might be taking a detour.

Could someone offer a hint or suggest a more strategic substitution or approach to make progress? Also, any general tips for recognizing what kind of methods to apply when you see problems involving radicals and polynomials like this?

Thanks in advance!

Rutvaj Nehete
  • 463
  • $x=2$ works..... – Will Jagy May 19 '25 at 00:32
  • $x=2\cos \theta$ will give you $\cos 3 \theta = \cos \dfrac{\theta}{2}$ – Hari Shankar May 19 '25 at 00:39
  • so the other real roots are $2 \cos \frac{4 \pi}{7}$ and $\frac{-1 - \sqrt5}{2}$ There are analogous roots to $x^3 - 3x = - \sqrt {x+2} $ – Will Jagy May 19 '25 at 00:45
  • 1
    What does the square root symbol even mean here? – Malady May 19 '25 at 00:47
  • What do you mean, it's just a regular square root... – Rutvaj Nehete May 19 '25 at 00:55
  • I believe that even the real solutions of this equation are quite complex—as evidenced when I attempted to compute them using Wolfram|Alpha. So here’s my suggestion: Let $y = \sqrt{x + 2}$. Substituting this into the equation, we obtain: $$x^3 - 3x - y - 3(y^2 - x - 2) = x^3 - 3y^2 - y + 6 = 0$$ Alongside the constraint: $$y^2 - x - 2 = 0$$ From this system, you can see that the complexity of solving for $x$ is significant. Indeed, by examining the Groebner basis of the system, one can appreciate just how intricate the solution structure for $x$ truly is. – Dang Dang May 19 '25 at 01:02
  • @RutvajNehete do you suspect that there is some nice form for the roots here? I don't see any specific reason why there ought to be. – Jonathan Beer May 19 '25 at 01:05
  • I will edit the post to include exactly the help I need. – Rutvaj Nehete May 19 '25 at 01:28
  • https://math.stackexchange.com/questions/2203364/solve-the-following-equation-x3-3x-sqrtx2 – lab bhattacharjee May 19 '25 at 03:09
  • 1
    The complex square root is two-valued. How is it supposed to be interpreted in the equation? Do you ask for solutions where we can choose any of the two square roots, so that it is effectively the same as $x^3-3x=\pm\sqrt{x+2}$? Or is it required to be a particular fixed branch of the square root, such as requiring the real part to be positive? – Emil Jeřábek May 19 '25 at 06:52
  • @RutvajNehete Please define a “regular square root” over $\mathbb{C}$. – Malady May 19 '25 at 12:21
  • Take only the principal, or positive, value, please. – Rutvaj Nehete May 19 '25 at 23:49

2 Answers2

4

The polynomial you get by squaring both sides and subtracting is $$ x^6 - 6x^4 + 9x^2 - x - 2 = (x-2)( x^2 + x - 1) (x^3 + x^2 - 2x - 1 ) $$

The cubic has roots $$ 2 \cos \frac{2 \pi}{7},2 \cos \frac{4 \pi}{7}, 2 \cos \frac{8 \pi}{7} $$

Three of the evident roots fit $x^3 - 3x = \sqrt{x+2},$ the other three fit $x^3 - 3x = - \sqrt{x+2},$

Further, all six roots are real.

enter image description here

About knowing the cubic polynomial see Reuschle(1875) https://archive.org/details/tafelncomplexer00unkngoog/page/n7/mode/2up Let me copy the appropriate page

enter image description here

Will Jagy
  • 146,052
  • 1
    How do you solve this without a calculator? And, more importantly, what is your inspiration, if any? – Rutvaj Nehete May 19 '25 at 01:32
  • @RutvajNehete From Will Jagy's solution, to solve that cubic equation, substitute $x= 2y$, and the analytical solution is here. – Dang Dang May 19 '25 at 01:43
  • 1
    @RutvajNehete there are brute-force methods to factorize integer coefficient polynomials: the constant term of factors must be divisors of original ones, then it is just finite cases to check. – Peter Wu May 19 '25 at 01:47
  • 1
    @DangDang see Reuschle(1875) https://archive.org/details/tafelncomplexer00unkngoog/page/n7/mode/2up – Will Jagy May 19 '25 at 01:48
  • @WillJagy Yes, I saw your addition and understand that the equation I provided was incorrect. – Dang Dang May 19 '25 at 01:59
1

Let $x=t^2+ \frac{1}{t^2}$ (note that there is always a complex $t$ for any complex $x$), then

$$\begin{cases}\text{LHS} = x^3-3x = t^6 + \frac{1}{t^6} \\ \text{RHS} = \sqrt{2+x} = \sqrt{(t+ \frac{1}{t})^2} = \pm (t+ \frac{1}{t}) \end{cases}$$

If necessary we can replace $t$ by $-t$, so we may assume $\sqrt{2+x} = t + \frac{1}{t}$.

Therefore, $$t^6 + \frac{1}{t^6} = t + \frac{1}{t}\Rightarrow t^6-t = \frac{1}{t} - \frac{1}{t^6}=\frac{t^6-t}{t^7}\Rightarrow t^6-t=0 \text{ or } t^7 = 1$$

Since $t\not=0$, $t^6-t=0$ can be simplified as $t^5=1$.

In either case, $t\mapsto t^2$ is a permutation of the $n$-th roots of unity (where $n=5, 7$ or any other odd integer), so we may assume $x = t + \frac{1}{t}$ for these $t$'s. Note that $t=\zeta$ and $t=\frac{1}{\zeta}=\bar\zeta$ yield the same $x=t + \frac{1}{t}$, hence in total there are six solutions corresponding to $t=1$, the two primitive $5$th-roots of unity on the upper half plane, and the three primitive $7$th-roots of unity on the upper half plane, in short,

$$t\in\{1, e^{\frac{2\pi i}{5}}, e^{\frac{4\pi i}{5}}, e^{\frac{2\pi i}{7}}, e^{\frac{4\pi i}{7}}, e^{\frac{6\pi i}{7}}\}$$

which correspond to $x=t+\frac{1}{t}=t+\bar{t}=2\cdot \mathrm{Re} (t)$,

$$x\in\{2, 2\cos\frac{2\pi}{5}, 2\cos\frac{4\pi}{5}, 2\cos\frac{2\pi}{7}, 2\cos\frac{4\pi}{7}, 2\cos\frac{6\pi}{7}\}$$

Just a user
  • 22,048