A good and simple approximation of the Riemann $\zeta$ function

Question

I have obtained, empirically, a very good and easy to express approximation of the Riemann $\zeta$ function inside the critical strip. The approximation is as follows (I give two versions, the second one being more complex, but also better by an order of magnitude in the constants involved):

$$A_1(\sigma+it)=\sum_{n=1}^{\lfloor t\rfloor}\frac{1}{n^{\sigma+it}}$$

$$A_2(\sigma+it)=\sum_{n=1}^{\lfloor t-1\rfloor}\frac{1}{n^{\sigma+it}}+\frac{1}{2}\sum_{n=\lfloor t\rfloor}^{\lceil t+1\rceil}\frac{1}{n^{\sigma+it}}$$

What surprised me is that this seems to be significantly better, computationally, than using the usual cutoff for the approximate functional equation of $t/(2\pi)$. In any case, I want to prove that the error of this approximation is small, of order $1/t^{\epsilon}$ for some $\epsilon>0$, inside the critical strip. Here is how I proceed (the idea given by @daniel’s answer in this post in this forum: How are Zeta function values calculated from within the Critical Strip?). The following is my not so good attempt at showing that the error, for $A_1,$ is small. Empirically, the error decreases as $t \to\infty$.

Using partial summation to obtain the first equality below, we have, for $\sigma>1$, that \begin{eqnarray} \sum_{n=1}^{\infty}\frac{1}{n^s}&=&s\int_1^{\infty}\frac{\lfloor x\rfloor}{x^{1+s}}dx=s \int_1^{\infty}\frac{ x}{x^{1+s}}dx - s\int_1^{\infty}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx\nonumber\\ &=&\frac{s}{s-1} -s\int_1^{\infty}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx\nonumber \end{eqnarray} so that \begin{eqnarray} \zeta(s)&=&\frac{s}{s-1} -s\int_1^{\infty}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx\quad (1)\label{exact} \end{eqnarray} with the integral converging for $\sigma>0$. On the other hand, from Euler's summation formula (see Jameson, The Prime Number Theorem, Proposition 1.4.6, P. 22) we get \begin{eqnarray*} \sum_{n=1}^{\lfloor t\rfloor}\frac{1}{n^s}&=&1+ \int_1^{t}\frac{ 1}{x^{s}}dx -s\int_1^{t}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx=1+\frac{t^s-t}{t^s (s-1)} -s \int_1^{t}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx \nonumber \end{eqnarray*} so that \begin{eqnarray} \sum_{n=1}^{\lfloor t\rfloor}\frac{1}{n^s}&=&1+\frac{1}{s-1}-\frac{t^{1-s}}{s-1}-s\int_1^{t}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx\quad (2)\label{inexact} \end{eqnarray} Moving the LHS in (2) to the RHS and then subtracting the resulting equality from (1) we get \begin{eqnarray*} \zeta(s)&=& \sum_{n=1}^{\lfloor t\rfloor}\frac{1}{n^s}+ \frac{t^{1-s}}{s-1}-s\int_t^{\infty}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx\quad (3) \end{eqnarray*} Thus, we have $$\left|\frac{t^{1-s}}{s-1}\right|=\left|\frac{t^{1-\sigma-it}}{\sigma-1+it}\right|=\frac{1}{t^{\sigma}}+o(1/t^{1/\sigma})$$ and $$\left|\int_t^{\infty}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx\right|=O(1/t^{\sigma}).$$

My problem is, I don’t know how to get rid of that $s$ factor multiplied with the integral in (3). Here are some pictures of the approximation $A_2$ vs $\zeta$, with the approximation by $A_1$ visibly as good, although not quite as good as $A_2$. Hopefully someone can help prove the error is small.

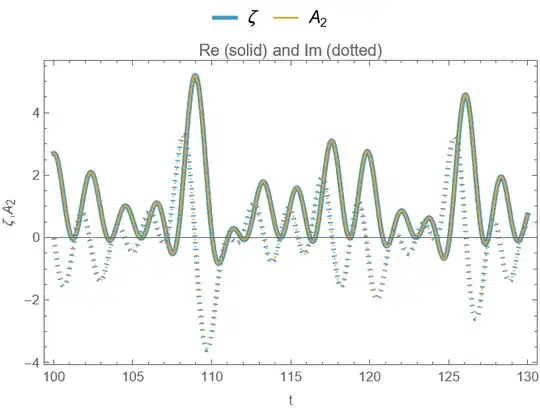$\zeta$ and the approximation $A_2$ " />

Answer 1

A desired approximation can be obtained by starting with the Abel-Plana formula instead. Suppose $x\ge2$ is not an integer. Then for $s=\sigma+it$, $\sigma>1$, there is

\begin{aligned} \sum_{n>x}{1\over n^s} &=\int_x^{+\infty}u^{-s}\mathrm du+\int_x^{x+i\infty}{u^{-s}\over e^{-2\pi iu}-1}\mathrm du+\int_x^{x-i\infty}{u^{-s}\over e^{2\pi iu}-1}\mathrm du \\ &={x^{1-s}\over s-1}+\int_x^{x+i\infty}{u^{-s}\over e^{-2\pi iu}-1}\mathrm du+\int_x^{x-i\infty}{u^{-s}\over e^{2\pi iu}-1}\mathrm du. \end{aligned}

As the right and side extends to an analytic function on $\mathbb C\setminus\{1\}$, we see that

\begin{aligned} E(s) &:=\zeta(s)-\left(\sum_{n<x}{1\over n^s}+{x^{1-s}\over s-1}\right) \\ &=\int_x^{x+i\infty}{u^{-s}\over e^{-2\pi iu}-1}\mathrm du+\int_x^{x-i\infty}{u^{-s}\over e^{2\pi iu}-1}\mathrm du \end{aligned} is valid for all $s$. Due to symmetry, we only lay out the details for treating $\int_x^{x+i\infty}$.

Let $u=x+iv$. Then \begin{aligned} \left|\int_x^{x+i\infty}\right| &=\left|\int_0^{+\infty}{e^{-s\log(x+iv)}\over e^{2\pi v-2\pi ix}-1}\mathrm dv\right|\le\int_0^{+\infty}{e^{-\sigma\log|x+iv|+t\arg(x+iv)}\over e^{2\pi v}-1}\mathrm dv \\ &\le x^{-\sigma}\int_0^{+\infty}{e^{|t|v/x}\over e^{2\pi v}-1}\mathrm dv\le2x^{-\sigma}\int_0^{+\infty}e^{-\left(2\pi-{|t|\over x}\right)v}\mathrm dv={2x^{-\sigma}\over2\pi-{|t|\over x}}. \end{aligned}

Conclusively, one has $$ |E(s)|\le{4x^{-\sigma}\over2\pi-{|t|\over x}}. $$ In particular, setting $x=|t|$ gives $E(s)=O(|t|^{-\sigma})$. Observe that at the same time $x^{1-s}/(s-1)=O(|t|^{-\sigma})$, so $$ \zeta(\sigma+it)=\sum_{n\le|t|}{1\over n^{\sigma+it}}+O(|t|^{-\sigma}). $$

Answer 2

As noted in comments, using the Fourier series of the sawtooth function $\psi(x)=x-[x]-1/2$ , we can give a direct proof that for $s=\sigma+it, 0<\sigma<A, t \ge 1$ and $y\ge Ct/(2\pi), C>1$ we have $$\left|s\int_y^{\infty}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx\right|=O_{A,C}(1/t^{\sigma})$$

We will fix $C>0, A>0$ now and just use $O$ though the implied dependencies will be quite clear.

We first note that $$\left|s\int_y^{\infty}\frac{1} {2x^{1+s}}dx\right|= \left|\frac{1}{2y^s}\right|=\frac{1}{2y^{\sigma}}$$ so up to allowable error we need to prove that $$\left|s\int_y^{\infty}\frac{\psi(x)} {x^{1+s}}dx\right|=O(1/t^{\sigma})$$

We have $$\psi(x)=-\sum_{k=1}^{\infty}\frac{\sin 2\pi kx}{k\pi}$$ with uniformly bounded partial sums so on any finite interval we can interchange summation and integration as long as we integrate against a continuous function say, so fixing a large $N>0$ we have $$s\int_y^N\frac{\psi(x)} {x^{1+s}}dx=C_1\sum_{k=1}^{\infty}\frac{s}{k}\int_y^N(e^{i(2\pi kx-t\log x)}-e^{i(-2\pi kx-t\log x)})x^{-1-\sigma}dx$$

Here $C_1$ is an absolute constant. We notice that since $x \ge y \ge Ct/(2\pi)$ we have $\frac{d}{dx}(2\pi kx-t\log x)=2\pi k-t/x \ge 2\pi (k-1)+\frac{(C-1)t}{x}> 2\pi(k-1), k \ge 2$ and also $2\pi -t/x \ge 2\pi (1-1/C)>0, k=1 $, so integrating by parts we get $$\int_y^N e^{i(2\pi kx-t\log x)}x^{-1-\sigma}dx=e^{i(2\pi kx-t\log x)}\frac{x^{-\sigma-1}}{(2\pi k-t/x)i}|_{y}^N+$$ $$+\int_y^N e^{i(2\pi kx-t\log x)}\frac{d}{dx}\frac{x^{-\sigma-1}}{(2\pi k-t/x)i}dx$$

Now for $k \ge 2$ the evaluation is clearly $O(\frac{y^{-\sigma}}{ky})$ so multiplying by $s/k$ and summing we get an $O(y^{-\sigma}\frac{|s|}{y}\sum_{k=2}k^{-2})$ hence using $|s|=O_A(t)$ and $2\pi y \ge Ct$ we clearly get the required $O(t^{-\sigma})$

For $k=1$ the evaluation is $O(\frac{y^{-\sigma}}{y(2\pi(1-1/C))}$) and again we are good.

For the integral term, we take absolute values and note that $-\frac{d}{dx}\frac{x^{-\sigma-1}}{2\pi k-t/x}>0$ so $$|\int_y^N e^{i(2\pi kx-t\log x)}\frac{d}{dx}\frac{x^{-\sigma-1}}{(2\pi k-t/x)i}dx|\le -\int_y^N \frac{d}{dx}\frac{x^{-\sigma-1}}{2\pi k-t/x}dx$$ which gives back the evaluation term above and the estimates we used show we again get $O(t^{-\sigma})$.

For the other term with $e^{i(-2\pi kx-t\log x)}$ we notice that the (absolute value of the) derivative is $2\pi k+t/x >2\pi k$ so we repeat the procedure noting that $x^{\sigma+1}(2\pi k+t/x)=2\pi kx^{\sigma+1}+tx^{\sigma}$ is still increasing since $\sigma >0, t>0$, while we do not need to separate in cases anymore.

Hence letting $N \to \infty$ our result is proved - actually we proved more, namely that for $s=\sigma+it, \sigma>0$ and $y\ge Ct/(2\pi), C>1$ we have $$\left|s\int_y^{\infty}\frac{x-\lfloor x\rfloor} {x^{1+s}}dx\right|=O_{C}(\frac{|s|}{y}\frac{1}{y^{\sigma}})+\frac{1}{2y^{\sigma}}$$