6

There was a question here a while ago about finding a positive integer sequence $a_n$ such that $\sin(a_n)$ converges. I saw somebody mention in the comments that you can find a sequence $a_n$ such that $\sin(a_n)$ monotonically tends towards $1$. I have no doubt that such a sequence exists, since there's this thread showing that $\sin(a_n)$ for $a_n=n$ is dense in $[-1,1]$, so there's obviously some subsequence you can pick out that's monotonic. However, is there any established formula for this? My intuition is leading me towards a no; if this sequence exists, the first few numbers are going to be $$a_1=1,a_2=2,a_3=8,a_4=14,a_5=33,...$$ I started questioning why $\sin(33)=0.999911...$ was so close to $1$, and realized that $33$ is peculiarly close to $\frac{21}{2}\pi$. I did the math and figured this is because $33 = \frac{21}{2} \cdot \frac{22}{7}$, one of the convergents of $\pi$'s continued fraction. But then, what about the earlier terms? What about $\frac{333}{106},\frac{355}{113}$, etc.?

Also, just as a bit of extra info, I calculated all the terms of this sequence that are lower than $10000$ in Python, and got this:

$$[1,2,8,14,33,322,366,699,1409,2119,2829,3539,4249,4959,5669,6379,7089,7799,8509,9219,9929]$$

Bizarrely, most of this sequence is such that the difference between consecutive terms is 710. Probably has something to do with $\frac{355}{113}$, since that's $355\cdot 2$.

So, to write my question down formally,

I am searching for a sequence $a_n$ such that $a_n \in \mathbb{Z}^+$ and $a_{n+1}$ is the smallest integer such that $\sin(a_{n+1})>\sin(a_n)$ $\forall \ n$. I suspect that this sequence is related to the $n$th convergent to $\pi$'s continued fraction. Is this suspicion correct, how are the two related, and is there a way to calculate the error in $1-\sin(a_n)$?

Thanks for the help!

Edit: some more testing with code virtually confirms that something fishy is going on with this sequence and the continued fraction for $\pi$. Define $b_n = a_{n+1}-a_n$. Then, $$b_1=1,b_2=6,b_3=6,b_4=19,b_5=289,b_6=44,b_7=333,b_8=710,b_9=710...$$ $$...b_{76}=710,b_{77}=104703$$ First off, what the heck's going on with $b_6$ where it's the only term that decreases? Second, $104703=103993+710$, and 103993 is the numerator of the fifth convergent to $\pi$. Can someone figure out what the relation between these two is?

Edit 2: After some testing, the difference $a_{n+1}-a_n$ seems to stay constant for random amounts of time until suddenly jumping to the next numerator of $\pi$ convergents. What are these intervals?? For reference, I've attached a graph of $a_n$ versus $n$ below: 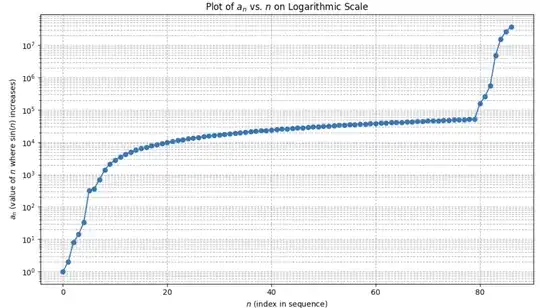blue graph for <span class=$a_n$ vs $n$" />

A line of constant slope gets bent into a logarithmic shape due to the logarithmic scale (the graph is completely unreadable using regular scale). It's starting to look like another stretch of constant $a_{n+1}-a_n$ is developing at the right, but I can't confirm this because my online compiler can't handle searching for values above $5\cdot 10^7$ very well.

Debalanced
  • 1,304
  • 2
  • 15
  • 3
    There are infinitely many sequences with this property, so to clarify, it seems like you specifically want to build the sequence greedily? As in, you want $a_{n+1}$ to be the smallest integer satisfying both $a_{n+1} > a_n$ and $\sin(a_{n+1}) > \sin(a_n)$? – nkm May 01 '25 at 16:15
  • For each $m,$ define $$f(m)=m-2\pi\lfloor m/2\pi\rfloor=m\bmod 2\pi$$ then the set $f(\mathbb N$'is dense in $[0,2\pi].$ So there are definitely such a sequence $a_n$ increasing such that $f(a_n)=\to\pi/2,$ and so $\sin(a_n)\to 1.$ Constructing such a sequence might be trickier. You might be able to do it by finding convergents for the continued fraction of $\pi.2,$ $p_k/q_k$ with $q_k\equiv 1\pmod 4, $ the take the next $a_n$ to be the next $p_k.$ But I know of no proof there are infinitely many such $k.$ It seems highly likely there is, since at least half of the $q_k$ are but. – Thomas Andrews May 01 '25 at 16:41
  • If you allow negative inters, we can find $a_n$ easily by letting $a_n=\pm p_k$ where the sign is chosen to make make $\sin(a_n)>0$ and $q_n$ is odd, for which it is easy to prove there are infinitely many. – Thomas Andrews May 01 '25 at 16:43
  • Related: https://math.stackexchange.com/q/5018106/42969, https://oeis.org/A046959 – Martin R May 01 '25 at 16:51
  • @nkm Yup! Trying to make every term in the sequence as small as possible – Debalanced May 01 '25 at 16:55
  • @MartinR darn, that didn't come up at all in my searches! the one I linked in the post was the only tangential one I found here. – Debalanced May 01 '25 at 16:57
  • @Debalanced: I computed the first elements (as you did), looked that sequence up in OEIS and then searched for A046959 on MSE :) – Martin R May 01 '25 at 16:59

1 Answers1

3

A constructive approach.

If $p_k/q_k$ are the convergents of the continued fraction for $\frac\pi2,$ then infinitely many $k$ have $q_k$ odd, since at least one of $q_k,q_{k+1}$ is always odd. Let $k_1,k_2,\dots,k_n,\dots$ be an increasing sequence such that all $q_{k_i}$ are odd.

We will first find a sequence $b_n$ such that $\sin(b_n)\to1,$ but not necessarily increasing.

Let $$b_{n}=\begin{cases}p_{k_n}&q_{k_n}\equiv1\pmod 4\\ 3p_{k_n}&q_{k_n}\equiv 3\pmod4 \end{cases}$$

Now, for any $k,$ $$d_k=|p_k-q_k\frac\pi2|<\frac1{q_k},$$ by known properties of continued fractions. So $d_k\to0.$ Also, if $q_k= 4m+1,$ then $$d_k=|p_k-2\pi k-\frac\pi2|<\frac1{q_k}$$ and so $$\sin(p_k)>\sin\left(\frac\pi2-\frac1{q_k}\right)$$

Likewise, if $q_k\equiv 3\pmod 4,$ then $3q_k=4m+1$ for some $m,$ ad you get $$\sin(3p_k)> \sin\left(\frac\pi2-\frac3{q_k}\right)$$

So you start with the continued fractions with odd denominators $$\frac11,\frac21,\frac{11}7,\frac{344}{219},$$

and get $$\{b_n\}=\{1,2,11\cdot 3,344\cdot 3,\dots\}$$

We can then find a subsequence $a_n=b_{k_n}$ for which $\sin(a_{n})$ is strictly increasing.

Martin R
  • 128,226
Thomas Andrews
  • 186,215
  • 2
    The next is a big jump $51819.$ That is because $\pi/2$ has a huge coefficient, $145$ in its continued fraction. – Thomas Andrews May 01 '25 at 17:42
  • $51819$ is interestingly the last term in my greedy version of the sequence before an even bigger jump to $156522$. If you're interested, I suppose I could add a list of all the terms I was able to calculate to the original question? – Debalanced May 01 '25 at 18:04
  • Well, the continued fraction numerators grow exponentially, so that "bigger jump" is only $3$ times bigger, but the jump from $344\cdot3$ to $51819$ is about$50$ times bigger. So "the jumps," in my algorithm at least, should be measured logarithmically. @Debalanced – Thomas Andrews May 01 '25 at 18:32
  • I've found that $a_{n+1}-a_n$ tends to stay constant for a long time before suddenly increasing to the next continued fraction of $\pi$ convergent numerator at weird intervals. My Colab notebook's struggling to handle an upper search limit above 10^7, but the last four sequence elements I found were [156522, 260515, 573204, 4846147]. – Debalanced May 01 '25 at 18:42
  • Yeah, when the $p_k/q_k$ is any continued fraction convergent, when $q_k$ is even and the next coefficient is $c_{k+1},$ then for $i=1,\dots,c_{k+1}-1,$ about $1/4$ of the values $ip_k+p_{k- 1}$ will be reasonably good guesses for the next highest $a_n,$ until you get $p_{k+1}.$ That would be my guess for the values that increase linearly. You'll get a long run of such cases when $c_{k+1}$ is big, as you get when the coefficient is $145.$ – Thomas Andrews May 01 '25 at 21:29
  • And when $c_k$ is small, the $p_k$ increase more slowly, although still exponentially. – Thomas Andrews May 01 '25 at 21:32
  • So, for example, when $q_7$ is even and $c_{k+1}=145,$ you get better and better $\sin((4j+1)p_7+p_6)=\sin(355(4j+1)+344)$ for $1\leq 4j+1\leq 145.$ – Thomas Andrews May 01 '25 at 21:43
  • Actually, you can replace $4j+1$ with $2j+1$ in that last comment. I forgot that $q_7$ being even means every other value will give a $\equiv1\pmod 4.$ So your long, linear run is almost certainly the $72$ values related to the large coefficient $145.$ You'll get such a run whenever $q_k$ is even and $c_{k+1}$ is large. Then yo uwill have a linear run of about $c_{k+1}/2$ or $c_{k+1}$ (depending on $q_k\bmod 4$) in a row which are improvements. But the coefficient $145$ is unreasonably large. – Thomas Andrews May 02 '25 at 18:59
  • It's certainly not impossible. The probability that $c_k>m$ for $k$ large is approximately $$\log_2\prod_{n\geq m}\frac{(n+1)^2}{n(n+2)}=\log_2(1+1/m)\approx\frac1{m\ln 2}$$ when $m$ is large. – Thomas Andrews May 02 '25 at 19:11
  • Interesting! So, does this mean eventually there will be a linear sequence that exceeds this "710 run" in length? – Debalanced May 02 '25 at 20:08
  • Probably, but that is just a heuristic - it will be true from "almost every" real number, in some sense that you will get arbitrarily large coefficients. We don't know much about the continued fraction coefficients of $\pi.$ There is certainly no reason to expect them to violate this rule. We know that $e$ has arbitrarily large coefficients, but that is because $e$ has a kind of regular continued fraction. – Thomas Andrews May 02 '25 at 20:24
  • When shen $c_{k+1}$ is large for the expansion of $e,$ $q_k$ is odd, so it seems like you won't get such a sequence then. – Thomas Andrews May 02 '25 at 20:28
  • Thank you! By the way, I mentioned in my edit that $b_6=a_7-a_6$ was the only part of the $b_n=a_{n+1}-a_n$ sequence I found that decreases from its previous term. Will there eventually be another term of the $b_n$ sequence that ends up decreasing, or is something special going on with $b_6$ in specific? – Debalanced May 02 '25 at 21:06