Integro-differential equation of one function of one variable with periodic condition

Question

I'm doing physics research and I have been able to boil down my problem to finding the general solution for $\xi(u)$ defined from 0 to 1. I am looking for periodic solutions, so $\xi(0)=\xi(1)$. I have no experience with these types of diff eqs so I don't really even know where to begin. $$-6\ddot\xi\int_0^1du \xi^{-2}+4m^2(-2\ddot\xi+2a^2\xi^{-3}c^2)=6\xi^{-3}\int_0^1du \dot\xi^2$$

If anyone could provide analytic tips/solutions that would be great, if this equation is too difficult for analytic solutions then Mathematica code for a numerical approximation would also be much apricated since I don't really know how to do numerical computations beyond "NIntegrate". Also $m$ is the mass and therefore positive, $a$ is a positive acceleration and $c$ is a real constant (it may break up into cases where $c>0, c<0,c=0$.

Thank you in advance.

Answer 1

You can discretize the equation by approximating the derivatives by finite differences and use numerical integration. Once you do that, you'll have a nonlinear system of equations that may be numerically solved by some fixed point algorithm (for instance Newton's method).

Setting up a grid of equally spaced points in $[0,1]$, say $u_i = i h$, with $h = \frac 1n$, the equation can be approximated by (I'm switching $\xi$ to $y$):

$$ -6 \dfrac{y_{i+1}-2y_1+y_{i-1}}{h^2} \sum_{i=0}^n \frac{w_i}{y_i^2}+4m\left( -2 \dfrac{y_{i+1}-2y_1+y_{i-1}}{h^2} + 2a^2c^2\sum_{i=0}^n \frac{w_i}{y_i^3}\right) = \frac{6}{y_i^3}\left(\frac{w_0(y_1-y_0)^2}{h^2} + \sum_{i=1}^{n-1} w_i \left(\frac{y_{i+1}-y_{i-1}}{2h}\right)^2 + \frac{w_n(y_n-y_{n-1})^2}{h^2}\right) $$

The coefficients $w_i$ depend on the quadrature rule that you use to approximate the integrals. In the case of the trapezoidal rule, they are given by $\frac h2, h, h, \cdots, h, \frac h2$. These equations are for the interior nodes. For the boundary nodes you must add two additional equations: One of them must be $y_0 - y_n = 0$, enforcing the periodic boundary conditions; The other can be a modification os the equation for interior nodes, but using forward (if using $u_0$) or backward (if using $u_n$) finite differences, in stead of the centred ones used before.

Finally, you just need to use your favorite solver to solve the system of nonlinear equations for the unknowns $y_0, \cdots, y_n$. Since you mentioned Mathematica, I suggest $\texttt{FindRoot[]}$.

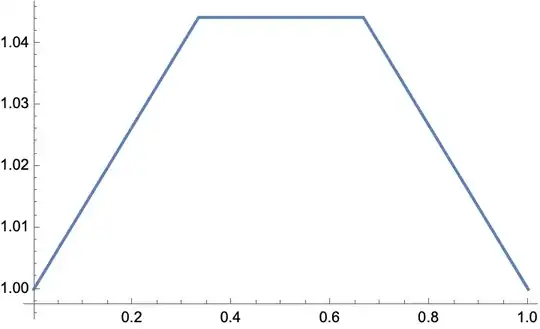
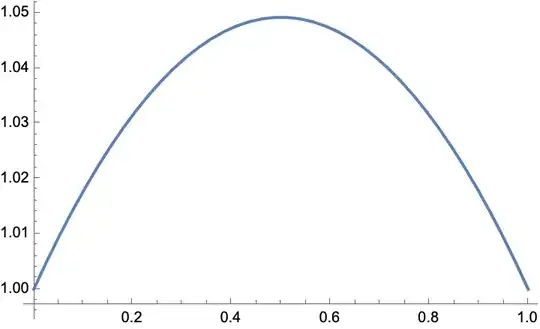
Below you can find the numerical solution using 4 grid nodes and 40 grid nodes. All the constants were set to 1 and, just out of laziness, I've set the last equation to $y_n=1$, instead of changing to backward differences.

Answer 2

We can actually solve this system analytically. I will use the same interpretation of the equation as in Pierre's answer, which by using brackets to clearly specify the integral is $$-6\ddot\xi\left(\int_0^1du \xi^{-2}\right)+4m^2(-2\ddot\xi+2a^2\xi^{-3}c^2)=6\xi^{-3}\left(\int_0^1du \dot\xi^2\right).$$ This equation can be written on the form $$\ddot{\xi} = \frac{A}{\xi^3},\tag{1}$$ where $$A = -\frac{6\int_0^1\dot{\xi}^2du-8a^2c^2m^2}{6\int_0^1\xi^{-2}du+8m^2}.\tag{2}$$ is a constant that depends on the solution. Lets first find some analytical solutions to this equation by ignoring the constraint on $A$ which we will treat as a free constant for now.

If we put $y = \xi^2$ then Equation 1 becomes $$2y\ddot{y} - \dot{y}^2 = 4A.\tag{3}$$ Taking the derivative of this equation we obtain $$2y\cdot \dddot{y} = 0$$ for which $y = Bx^2+Cx+D$ follows. Inserting this back into Equation 3 we get the constraint $D = \frac{4A + C^2}{4B}$ and the general solution is therefore $$y = B\left(x+\frac{C}{2B}\right)^2 + \frac{A}{B}.$$ Next imposing $y(0) = y(1)$ we get $C = -B$ and $$\xi(u) = \pm\sqrt{\frac{A}{s} + s(u-1/2)^2},$$ where $s$ ($B$ above) is a free constant (determined by the initial condition $\xi(0)^2 = \frac{A}{s} + \frac{s}{4}$). Note that the solution shown in Pierre's answer corresponds to taking $A \simeq -0.44$ and $s\simeq -0.40$.

We can now evaluate the constant $A$ by plugging this solution into Equation 2 and performing the integrals. This gives us an equation for $A$ which we can solve. The integrals turns out to be tractable (they are on the form $\int\frac{ax+bx}{cx^2+dx+e}dx$), just a bit tedious to evaluate so I used Mathematica and it gave the simple equation $$A = a^2c^2 - \frac{3s}{4m^2},$$ and we are left with a full family of solutions $$\xi_s(u) = \pm\sqrt{\frac{a^2c^2}{s} - \frac{3}{4m^2} + s(u-1/2)^2},$$ parametrized by $s$ (or equivalently $\xi(0)$). Note that we need to impose $0 < s < \frac{4a^2c^2m^2}{3}$ to avoid a negative square root.

Verification of the solution in Mathematica:

(* Define the general solution *)
f[x_] = Sqrt[A/s + s (x - 1/2)^2];
(* You can also find this solution by using DSolve on y'' = A/y^3 *)
DSolve[{y''[x] y[x]^3 == A, y[0] - y[1] == 0}, y, x]
(* Evaluate the two integrals in the ODE *)
c1 = Assuming[s [Element] Reals && A [Element] Reals && A > 0 && s > 0, Integrate[1/f[x]^2, {x, 0, 1}]];
c2 = Assuming[s [Element] Reals && A [Element] Reals && A > 0 && s > 0, Integrate[f'[x]^2, {x, 0, 1}]];
(* Solve for A *)
sol = Solve[-6 f''[x] c1 + 4 m^2 (-2 f''[x] + 2 a^2 c^2/f[x]^3) - 6 c2/f[x]^3 == 0, A];
(* The solution with the correct A value (prints the same solution as in the answer) *)
g[x] = f[x] /. sol

Answer 3

No, a solution to such a complicated functional probably does not exist. By the standard energy method of second order equations of motion we get

$$\begin{align}& \xi ''(t)-\frac{a^2 c^2}{\xi (t)^3}+\frac{3}{2 m^2} \ \int_0^1 \left(\frac{\xi ''(t)}{\xi (u)^2}+\frac{\xi '(u)^2}{\xi (t)^3}\right) \, du \ = \ 0 \\&\xi '(t) \xi ''(t) -\frac{a^2 c^2 \xi '(t)}{\xi (t)^3}+\frac{3}{2 m^2} \ \int_0^1 \left(\frac{\xi '(t) \xi '(u)^2}{\xi (t)^3}+\frac{\xi '(t) \xi ''(t)}{\xi (u)^2}\right) \, du \ = \ 0 \\& \frac{\partial }{\partial t}\frac{1}{2} \left(\xi '(t)^2 +\frac{a^2 c^2}{\xi (t)^2}+\frac{3}{4 m^2} \ \int_0^1 \left(\frac{\xi '(t)^2}{\xi (u)^2}-\frac{\xi '(u)^2}{\xi (t)^2}\right) \, du\right)=0 \\& \frac{1}{2} \left(\xi '(t)^2+ \frac{a^2 c^2}{\xi (t)^2}+\frac{3}{4 m^2} \ \int_0^1 \left(\frac{\xi '(t)^2}{\xi (u)^2}-\frac{\xi '(u)^2}{\xi (t)^2}\right) \, du\right)=e=\text{const} \end{align},$$ physically a very uncommon expression for a energy. Perhaps it would be helpful to give a hint of its orgin.

Algebraic form and the factor 6 point to a form of a deformed Korteweg-de Vries equation for 1d surface waves.