Product of monoids in a braided monoidal category

Question

Given two monoids $(A, \mu_A, \eta_A)$ and $(B, \mu_B, \eta_B)$ in a braided monoidal category $(\mathcal{C}^{\otimes}, \gamma)$, is $A \otimes B$ a monoid as well with the following structure map? 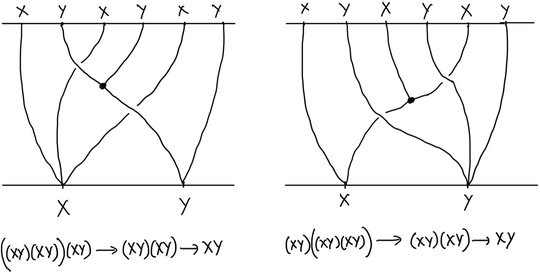$$(A \otimes B)\otimes (A \otimes B) \to A \otimes(B \otimes (A \otimes B)) \to A \otimes ((B \otimes A)\otimes B) \xrightarrow[]{\gamma} A \otimes ((A \otimes B)\otimes B) \to A \otimes(A \otimes (B \otimes B)) \to (A \otimes A) \otimes (B \otimes B) \xrightarrow[]{\mu_A \otimes \mu_B} A \otimes B$$ and, $$I \to I \otimes I \xrightarrow[]{\eta_A \otimes \eta_B} A \otimes B$$ Here are the two string diagrams $(A=X, B=Y)$ for the two composites $$((A \otimes B)\otimes (A \otimes B))\otimes (A \otimes B) \to (A \otimes B)\otimes (A \otimes B) \to A \otimes B$$ and $$(A \otimes B)\otimes ((A \otimes B))\otimes (A \otimes B)) \to (A \otimes B)\otimes (A \otimes B) \to A \otimes B $$ which essentially seems to be same upto deformation. But it is not so clear if the underlying braidings are also the same, or not.

Answer 1

Yes. We need two ingredients for this:

1. In a braided monoidal category, the tensor product functor $- \otimes - : \mathcal{C} \times \mathcal{C} \to \mathcal{C}$ is monoidal; see theorem 5.3.4 in Geoff Cruttwell's PhD thesis. In fact this is true in any monoidal category satisfying a certain "middle-four interchange" condition, which includes braided categories; see the agda-categories library (here and here) for a formalised proof in Agda.
2. Monoidal functors preserve monoids; this is standard but see 1Lab for a formalised proof in Agda.

If $A$ and $B$ are monoids in $\mathcal{C}$ then $(A, B)$ is a monoid in $\mathcal{C} \times \mathcal{C}$, so the above implies that $A \otimes B$ is a monoid with the structure maps you mentioned.