In January 2022, MathOverflow user pregunton commented that it is possible to enumerate all rational numbers using iterated maps of the form $f(x) = x+1$ or $\displaystyle g(x) = -\frac 1x$, starting from $0$.
Let $X_n$ be the rational numbers can be generated from $n$ steps of this process (and no fewer) and let $|X_n|$ be the size of this set.
For instance $-2 \in X_5$ because there is a length-$5$ chain of these functions that maps $0$ to $-2$: $g\circ f\circ g\circ f\circ f(0) = -2$. $$0 \overset{f}{\longmapsto} 1 \overset{f}{\longmapsto} 2 \overset{g}{\longmapsto} -\frac12 \overset{f}{\longmapsto} \frac 12 \overset{g}{\longmapsto} -2$$
A tree and a table of $X_n$.
Here's an illustration of the growth process.
Here are the numbers in a table: $$ \begin{array}{c|l|c} n & X_n & |X_n| \\ \hline n=0 & \{0\} & 1 \\ n=1 & \{1\} & 1 \\ n=2 & \{-1, 2\} & 2 \\ n=3 & \{-\frac12, 3\} & 2 \\ n=4 & \{-\frac13,\frac12,4\} & 3 \\ n=5 & \{-2,-\frac14,\frac23,\frac32, 5\} & 5 \\ n=6 & \{-\frac32,-\frac23,-\frac15,\frac34, \frac53, \frac52, 6\} & 7 \\ n=7 & \{-\frac43,-\frac35,-\frac25,-\frac16,\frac13,\frac45,\frac74,\frac83,\frac72,7\} & 10 \end{array} $$
The first $26$ terms of the $0$-indexed sequence of $|X_n|$ begins $$1, 1, 2, 2, 3, 5, 7, 10, 15, 22, 32, 47, 69, 101, 148, 217, 318, 466, 683, 1001, 1467, 2150, 3151, 4618, 6768, 9919, \dots,$$
which for $n\geq4$ satisfies the recurrence $$|X_n| = |X_{n-1}| + |X_{n-3}|.$$
Question: why this recurrence?
A reasonable conjecture is that the sequence of $|X_n|$ always satisfies the above linear recurrence. Is there a combinatorial (or non-combinatorial) way to see why?
(Note: a similar conjecture appears in OEIS sequence A226136.)
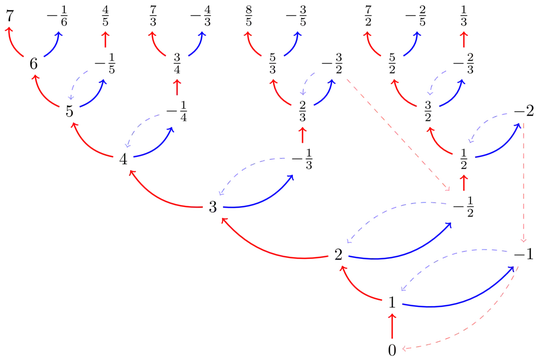
For $n > 1$, let $F_n$ and $G_n$ be the number of terms in $X_n$ that were generated by $f$ and $g$ respectively. Then it appears that for $n \ge 2$, $|F_n| = |G_{n+1}| = A000930(n-1)$, where A000930 is Narayana's cows sequence: $a(0) = a(1) = a(2) = 1$; thereafter $a(n) = a(n-1) + a(n-3)$.
Still curious for an explanation why!
– Peter Kagey Apr 20 '25 at 16:09