5

I am studying about the center of the mapping class group of a genus $g$ surface. I am having some difficulties in understanding the proof for the triviality of the group $Z(Mod(S_{g}))$. Here is the proof:

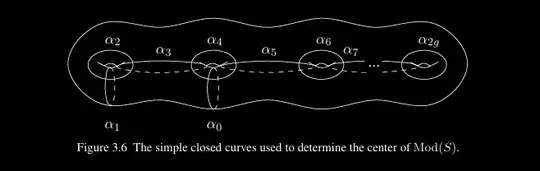
enter image description here

Proof. Any central element $f$ of $\operatorname{Mod}\left(S_{g}\right)$ must fix every isotopy class of simple closed curves in $S_{g}$. Consider the simple closed curves $\alpha_{0}, \ldots, \alpha_{2 g}$ shown in Figure 3.6. By statement 1 of the Alexander method, $f$ has a representative $\phi$ that fixes the graph $\cup \alpha_{i}$, and thus $\phi$ induces a map $\phi_{*}$ of this graph.

enter image description here

The graph $\cup \alpha_{i}$ is isomorphic to the abstract graph $\Gamma$ shown in Figure 3.7 for the case $g=4$. For $g \geq 3$, the only automorphisms of $\Gamma$ come from flipping the three edges that form loops and swapping pairs of edges that form loops. The collection of simple closed curves in Figure 3.6 form a graph in $S_{4}$ that is abstractly isomorphic to the graph $\Gamma$ shown here for the case $g=4$. form a loop. In particular, any automorphism of $\Gamma$ must fix the three edges coming from $\alpha_{4}$. Thus we see that $\phi$ preserves the orientation of $\alpha_{4}$, and so since $\phi$ is orientation-preserving, it must also preserve the two sides of $\alpha_{4}$. It follows that $\phi_{*}$ does not flip the edge of $\Gamma$ coming from $\alpha_{0}$, and it does not interchange the two edges coming from $\alpha_{3}$ or the two coming from $\alpha_{5}$. Inductively, we see that $\phi_{*}$ fixes each edge of $\Gamma$ with orientation. By statement 2 of the Alexander method, plus the fact that the $\left\{\alpha_{i}\right\}$ fill $S_{g}$, we have that $\phi$ is isotopic to the identity; that is, $f$ is the identity.

My Question: 1) What does the author mean by orientation of $\alpha_{4}$. To begin with $\alpha_{i}$'s don't have a sense of direction in them, right?

2)What does the author mean when he says "since \phi is orientation preserving it must preserve the two sides of $\alpha_{4}$, what are sides of a curve?

3)How does it follow that $\phi_{*}$ does not flip the edge coming from $\alpha_{0}$, nor it does it interchange the edges coming from $\alpha_{3}$ or the two coming from $\alpha_{5}$?

These are the steps where I got stuck , if I am able to satisfy myself with these questions, I would have understood this whole proof. Any help would be appreciated. Thanks !

Dwaipayan Sharma
  • 604
  • All of these curves live in the fundamental group of $S_g$, which is made entirely of oriented loops. If one deletes $\alpha_4$, this produces two new boundary components, a regular neighborhood of each of which can be arbitrarily labelled the "inside" and the other the "outside". In the abstract graph, there are three "X"s with vertices on the circle corresponding to $\alpha_4$. These are three little neighborhoods on the handlebody, each having two little "arms" on the "inside" and two on the "outside" of $\alpha_4$. Interchanging the $\alpha_0$ edge would relabel its edges incoherently. – Eric Towers Apr 15 '25 at 06:14
  • @EricTowers Sorry I don't think I could follow. What does it mean by "deleting $\alpha_{4}$". Do you mean cutting along $\alpha_{4}$? – Dwaipayan Sharma Apr 15 '25 at 06:40
  • Yes. Pick a representative for $\alpha_4$ from the equivalence class of loops in the fundamental group, e.g., the one in the diagram. When you delete the points in that loop, you obtain two new (open) boundary components. A small neighborhood of each component is an annulus. Label one annulus "inside" and one "outside". Alternatively, label the one that $\alpha_4$ circumnavigates in the positive direction "inside" and the one it circumnavigates in the negative direction "outside". – Eric Towers Apr 16 '25 at 18:31

0 Answers0