Envelope of the function $f(x)=\frac{\sin(x)}{\sin(x/N)}$

Question

Given a positive integer $N$, let us consider the function $$ f(x)= \frac{\sin(x)}{\sin(x/N)} $$ in the interval $0<x<2\pi N$. What is the envelope function of $f$ ?

My attempt I know that $1/x$ is an envelope function of $\operatorname{sinc}(x)=\frac{\sin x}{x}$. Can this fact help me since $f(x)=\frac{\operatorname{sinc}(x)}{N\operatorname{sinc}(x/N)}$?

Answer 1

Here is a very plain solution :

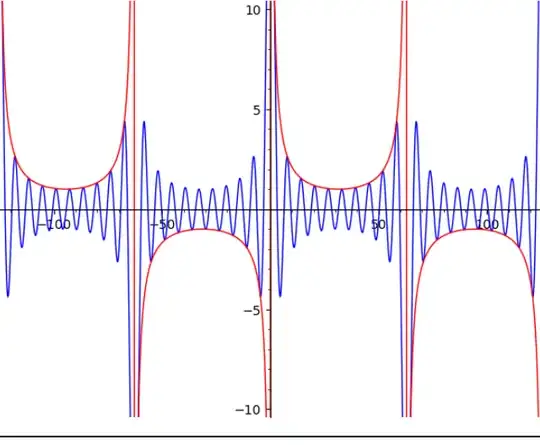
Fig. 1 : case $N=20$.

The blue curve represents

$$f_N(x)=\frac{\sin(x)}{\sin(x/N)}$$

The red curve represents what you call its envelope, which has the following equation :

$$g(x)=\frac{1}{\sin(x/N)}$$

Up to you for the very simple explanation...

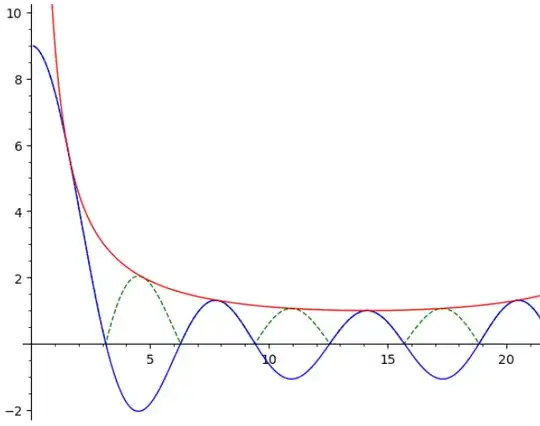
Fig. 2 : Zooming on Fig. 1. The dotted curve represents the absolute value of $g$ which is also tangent to the curve of $f_N$.

Remarks :

1. Changing $f_N(x)$ into $f_N(Nx)=\frac{\sin(Nx)}{\sin(x)}$, one gets an "avatar" of the so-called Dirichlet kernel.

2. The complete envelope is in fact given by $\pm g(x)$.

3. See this article available on ResearchGate entitled "Multi-Frequency Phase Synchronization" by Tingran Gao, in particular its Fig. 7.

Answer 2

As a rule, since the functions $\pm{1}$ form the envelope of $\sin x$, in the same way $\pm f(x)$ form the envelope of $f(x) \sin x$. It just works..