Se cube
Given an $n$-sphere of radius $1$, we can construct the $n$-cube that exscribes it as having half-side-length $1$, and the $n$-cube that inscribes it as having a half-side-length of $1/\sqrt{n}$. Between these two $n$-cubes is one that splits the difference between them and best approximates the sphere (specifically, such that the average distance from the center to the cube over an directions given an even spherical weighting is as close as possible to $1$).
—
Some low-dimensional examples:
In one dimension: The $1$-cube with half-length $\ell$ has a mean radius of $$\bar{r} = \ell,$$ so the $1$-cube that best approximates the $1$-sphere has length $\ell=1$.
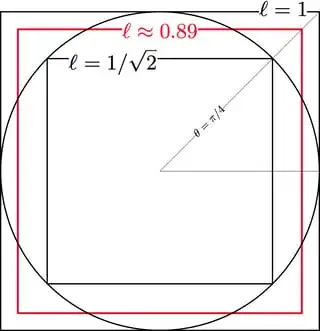
In two dimensions: The unit $2$-cube has an angular mean radius of $$ \bar{r} = \frac{1}{\pi/4}\int_{0}^{\pi/4} \frac{1}{\cos \theta}\, d\theta \approx 1.12,$$ so the $2$-cube that best approximates the unit two-sphere has $$\ell = \frac{1}{\bar{r}} \approx 0.89,$$ as illustrated in the diagram below.
Is there a standard formula for the size of this cube? It seems like it should be possible to generalize the two-dimensional solution (at least to the point of providing an integral that can be evaluated numerically), but it’s a side problem to the work I’m actually doing, and is likely to have some traps in properly weighting the spherical integrals. I’d rather have something I can cite and avoid reinventing the wheel than to dive down this rabbit hole.
Searches haven’t come up with anyone even asking the question I’m looking at, so I’m not sure if it normally gets asked under different terminology.