How to find the area of this irregular polygon if only given the side lengths?

Question

For a long time, I've been trying to create an extension of the polygon function, similar to how the gamma function is an extension of the factorial function.

The way it works is that it grows from lets say a regular 9-gon to a regular 10-gon, 9 sides are fixed in length whilst the 10th side grows from length zero to the same length of the other 9 sides, then it would go from a 10 to 11-gon with 10 sides being fixed in length whilst the 11th side grows from length zero to the same length of the other 10 sides, etc, etc.

The normal regular polygon formula works by dividing a full rotation by the number of sides to get the exterior angle to calculate the area, but this method doesn't work when it's growing between 2 regular polygons (also when the growing polygon has a perimeter of lets say 6.5 (6 sides length 1, 1 side length 0.5) the exterior angle measured from the non growing sides doesn't equal (360/6.5) degrees like you'd expect).

These growing polygons always have some special properties no matter what stage of growth they're at that set it apart from the other irregular polygons, which I believe if said properties are exploited it might make it possible to solve for the area for them when only given the side lengths. These properties are:

• They're always circumscribable (all vertices always lie on a circle)

• When a circle is inscribed inside this polygon, the circle always touches the midpoints of all the sides with fixed lengths but doesn't touch the growing side (unless the growing side is the same length as all the non growing sides but by then it's redefined as a non growing side)

• The perpendicular bisectors of all sides (including the growing side) always pass through the centre point of both the inscribed and circumscribing circle

• Based off the previous bullet point, both of those circles always share the same centre point

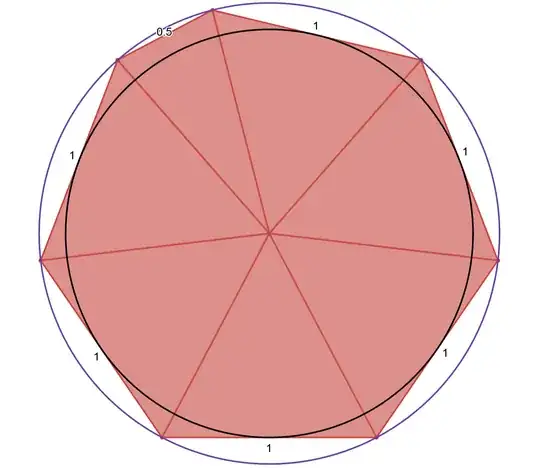
So now with all of this information, the polygon I want to find the area of is the image below. It's a 6-gon growing to a 7-gon with 6 sides with length 1 and the 7th side with length 0.5. I would also love to know as a bonus the radius of the polygon and any angles if possible.

I know that it looks like I'm asking the same question as I did in this post I created a continuously growing polygon. However, I can't figure out how to calculate its area if I only know the perimeter. but this time I'm asking how to find the area, radius and angles of the shape in the image in this post only based off of the information given in this post.

Answer 1

As the length $L$ of the new side increases, so does the central angle it subtends. If there were originally $n$ sides, this shinks the $n$ other centrail angles, and if the circumcircle were of constant radius, would mean the other $n$ sides would decrease as well. To keep them at a length of $1$, the radius of the circumcircle must grow enough to compensate. But that growth also would mean that the original $L$ would grow as well. Instead of trying to trace this off of $L$, I suggest instead working with the central angle $2\theta$ subtended by the new side (having $\theta$ be half the central = angle makes the formulas a little nicer).

For a given value of $\theta$, since the remaining $n$ central angles are the same size, they must be $\frac{2(\pi - \theta)}n$. In a circle of radius $R$, the length of a chord subtending a central angle of $2\phi$ is $$2R\sin \phi$$ So to keep the length $1$, we must have $$R = \dfrac 1{2\sin\left(\dfrac {\pi - \theta}n\right)}$$ and $L$ is given by $$L = \dfrac{\sin \theta}{\sin\left(\dfrac {\pi - \theta}n\right)}$$

The distance of a chord subtending an angle of $2\phi$ from the center is $R\cos\phi$, which means the area of the triangle formed by the chord and the center is $$A(\phi) = R^2\sin\phi\cos\phi = \frac12 R^2\sin{2\phi}$$

For the $n$ sides of length $1$, $R$ was chosen so that $R\sin\phi = \frac 12$, so the triangles subtended by those $n$ sides have area $$A_T\left(\frac{\pi - \theta}n\right) = \frac 14\cot\left(\dfrac {\pi - \theta}n\right)$$ The triangle for the new side has area $$A_T(\theta) = \dfrac{\sin 2\theta}{8\sin^2\left(\dfrac {\pi - \theta}n\right)}$$

The area of the polygon is the sum of the areas of these central triangles, so $$A_P(\theta) = \frac n4\cot\left(\dfrac {\pi - \theta}n\right) + \dfrac{\sin 2\theta}{8\sin^2\left(\dfrac {\pi - \theta}n\right)}$$

The $\theta$ for which $A_P(\theta)$ takes on a particular value such as $\pi$ is not going to be obtainable by some nice neat formula, but Newton's method will converge quickly. And once you have a good approximation for $\theta$, $L$ and $R$ can be obtained from the formulas above.