Probability of non-intersecting Polya Urn sequences

Question

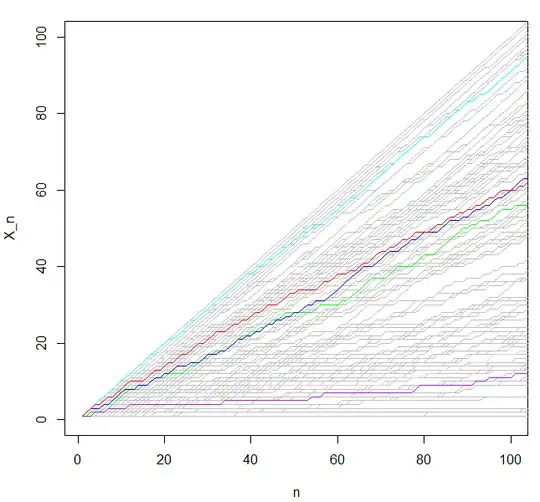
Suppose you have a standard Polya Urn process: as the initial step you have $1$ red ball and $1$ blue ball in an urn; at further each step you draw a ball and then replace it together with another ball of the same colour, so at step $n+1$ (i.e. after $n$ draws) you have $X_{n+1}$ red balls and $n+2-X_{n+1}$ blue balls where $P(X_{n+1} = k+1 \mid X_{n}=k)= \frac{X_{n}}{n+1}$ and $P(X_{n+1} = k \mid X_{n}=k)= \frac{n+1-X_{n}}{n+1}$, starting with $X_1=1$; the marginal distribution of $X_n$ is discrete uniform on $\{1,2,\ldots,n\}$ each with probability $\frac{1}{n}$ and so $\frac{X_n}{n+1}$ converges in distribution to being continuous uniform on $(0,1)$.

Let's call $\mathbf{X}=\left(X_1,X_2,X_3, \ldots\right)$ a Polya Urn sequence, and let's take $\mathbf{Y}=\left(Y_1,Y_2,Y_3, \ldots\right)$ and $\mathbf{Z}=\left(Z_1,Z_2,Z_3, \ldots\right)$ as two independent Polya Urn sequences. What is the probability that $\mathbf{Y}$ and $\mathbf{Z}$ do not meet again i.e. $\mathbb P(\nexists n\gt 1: Y_n =Z_n \ )$, and what is the probability that $\mathbf{Y}$ and $\mathbf{Z}$ do not cross i.e. $\mathbb P(\nexists n,m: Y_n >Z_n \cap Y_m < Z_m\ )$?

Simulation suggests:

• $\mathbb P(\nexists n\gt 1: Y_n =Z_n \ ) \approx 0.333$. Is this exactly $\frac13$?
• $\mathbb P(\nexists n,m: Y_n > Z_n \cap Y_m < Z_m\ ) \approx 0.713$. What is this more precisely?

Here is an example of a simulation using R (I did more and extrapolated to estimate the result for infinite sequences):

PUsequence <- function(maxn){
  X <- 1
  for (n in 1:(maxn-1)){
    X[n+1] <- X[n] + rbinom(1, 1, X[n]/(n+1))
    }     
  X
  }
abovebelow <- function(maxn){
  Y <- PUsequence(maxn)
  Z <- PUsequence(maxn)
  c(sum(Y-Z > 0), sum(Y-Z < 0))
  }
set.seed(2025)
maxn <- 2^9
cases <- 10^5
sims <- replicate(cases, abovebelow(maxn))
mean(sims[1,] == maxn-1 | sims[2,] == maxn-1)
0.33285
mean(sims[1,] == 0 | sims[2,] == 0)
0.71513

and the initial parts of some simulated paths

Answer 1

Here are some calculations. I don't know if you can make something out of it.

For all $k<n$, for all $0\le i\le k <n$ and $i\le j\le n-k+i$, $$\mathbb P(X_n=j|X_k=i)=\frac{(j-1)!(n-j)!k!}{(i-1)!(k-i)!n!}\binom{n-k}{j-i}=\frac{i\binom ki\binom{n-k}{j-i}}{j\binom nj}$$ Then by independence of $X_n$ and $Y_n$, $$\mathbb P(X_n=Y_n=j|X_k=Y_k=i)=\frac{i^2\binom ki^2\binom{n-k}{j-i}^2}{j^2\binom nj^2}$$ with the special case $$\mathbb P(X_n=Y_n=j)=\frac{1}{n^2}$$

Note $A_{n,j}=\{X_n=Y_n=j\}\cap\{\forall 1<k<n,X_k\neq Y_k\}$. Then $$\mathbb P(A_{n,j})=\mathbb P(X_n=Y_n=j)-\sum_{k=2}^{n-1}\sum_{i=1}^{\min(k,j)}\mathbb P(A_{k,i})\mathbb P(X_n=Y_n=j|A_{k,i})$$ $$j^2\binom nj^2\mathbb P(A_{n,j})=\binom{n-1}{j-1}^2-\sum_{k=2}^{n-1}\sum_{i=1}^{\min(k,j)}i^2\binom ki^2\mathbb P(A_{k,i})\binom{n-k}{j-i}^2$$

We can note $c_{k,i}=i^2\binom ki^2\mathbb P(A_{k,i})$ so that $$c_{n,j}=\binom{n-1}{j-1}^2-\sum_{k=2}^{n-1}\sum_{i=1}^{\min(k,j)}c_{k,i}\binom{n-k}{j-i}^2$$

Answer 2

Let the two Polya urns sequences be $(X_n)_{n=0}^\infty$ and $(Y_n)_{n=0}^\infty$.

Denote

$$ C(a,b,n) = \mathbb P (X_n = a, Y_n = b \text{ and } \forall j\in [1\dots n]:X_j\leq Y_j) $$

The second question's answer is $$ 2\left( \sum_{b=1}^{n+1} \sum_{a=1}^b C(a,b,n) \right) - \mathbb P \left(\forall j\in [1\dots n]:X_j = Y_j \right) $$

but since $\mathbb P \left(\forall j\in [1\dots n]:X_j = Y_j \right)$ is clearly vanishingly small as $n\to \infty$, it suffices to consider only the first thing.

Introduce the generating function

$$ G(x,y,z) = \sum_{n=0}^\infty \sum_{b=1}^{n+1} \sum_{a=1}^b C(a,b,n)x^ay^bz^n. $$

From the recursion

$$\begin{aligned} C(a,b,n) = \frac{(n+1-a)(n+1-b)}{(n+1)^2} & C(a,b,n-1) \\ + \frac{(n+1-a)(b-1)}{(n+1)^2} & C(a,b-1,n-1) \\ + \frac{(a-1)(n+1-b)}{(n+1)^2} & C(a-1,b,n-1) \\ + \frac{(a-1)(b-1)}{(n+1)^2} & C(a-1,b-1,n-1) \end{aligned}$$

(which we get by considering what can happen in the urns in one step) and using the following, which seems to be true

Lemma 1

$$ \sum_{n=0}^\infty \sum_{b=1}^{n+1} b(n+2-b)C(b,b,n) x^ay^bz^n = \frac{xy}{z(1-xy)}\log\left( \frac{1-xyz}{1-z} \right) $$

we get the following by multiplying with $x^ay^bz^n$ and summing (Lemma 1 is used when we do $a$-index shift in the third sum on the right and those are the terms we miss out from the full sum)

$$ z^2(1-z) G_{zz} + xz^2(1-x)G_{xz} + yz^2(1-y)G_{yz} - xyz(1-x-y+xy)G_{xy} \\ + 2xz(1-x)G_{x} + 2yz(1-y)G_{y} + z(3-5z)G_{z} + (1-4z)G \\ = xy - \frac{x^2y}{1-xy}\log\left( \frac{1-xyz}{1-z} \right). $$

This equation is horrible, but luckily we're interested in $G(1,1,z)$ so plugging in $x=y=1$ reduces it to (we need to make $\frac{1}{1-xy}\log\left( \frac{1-xyz}{1-z} \right) \to \frac{z}{1-z}$ on the right hand side)

$$ z^2(1-z) G_{zz} + z(3-5z)G_{z} + (1-4z)G = \frac{1-2z}{1-z}. $$

From this we get the simple recursion for $c_n = [z^n]G(1,1,z)$:

$$ c_0 = 1 \\ c_n = c_{n-1} - \frac{1}{(n+1)^2}. $$

So

$$ \lim_{n\to \infty} c_n = 1 - \sum_{n=1}^\infty \frac{1}{(n+1)^2} = 2 - \frac{\pi^2}{6} $$

and the answer is twice that i.e.

$$ \boxed{ 4 - \frac{\pi^2}{3} \approx 0.7101318663 } $$

---

With the following lemma

Lemma 2

$$ \mathbb P \left(\forall j\in [1\dots n]:X_j = Y_j \right) = \frac{1}{(n+1)^2}\sum_{j=0}^{n} \frac{1}{\binom{n}{j}} $$

we get an exact expression for the probability of not crossing after $n$ steps:

$$ 4 - 2\sum_{j=0}^{n} \left( \frac{1}{(j+1)^2} + \frac{1}{2(n+1)^2 \binom{n}{j}} \right) $$