Can a Function’s Derivative Oscillate More Than the Function Itself?

Question

In calculus, I’ve seen derivatives either smooth out or amplify a function’s behavior. For instance, with $f(x) = \sin(x)$, the derivative $f'(x) = \cos(x)$ oscillates just like the original, both staying between $-1$ and $1$. But could the derivative oscillate more? I tested $f(x) = x \sin(x)$,

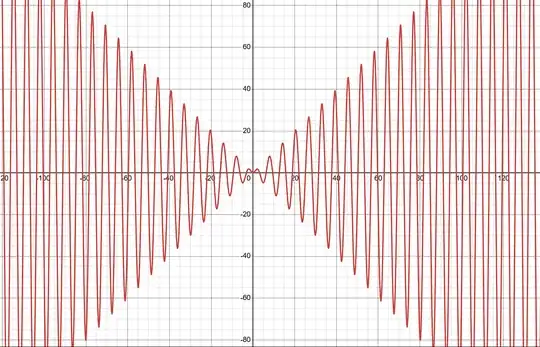
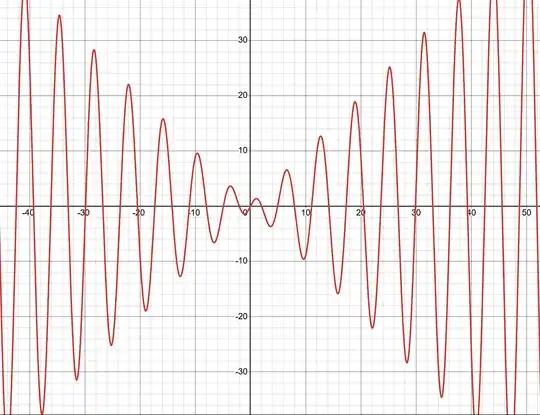
where $f'(x) = \sin(x) + x \cos(x)$. At $x = 2\pi$, $f(2\pi) = 2\pi \sin(2\pi) = 0$, yet $f'(2\pi) = \sin(2\pi) + 2\pi \cos(2\pi) = 2\pi \approx 6.28$. Plotting the graph of the derivative, I get

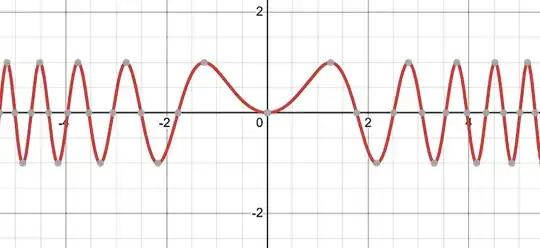
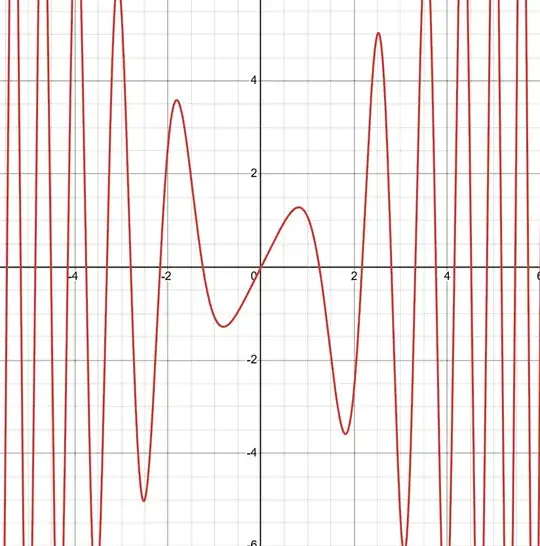
$f(x)$ wiggles with peaks that grow, while $f'(x)$ swings wider. Then, with $f(x) = \sin(x^2)$, $f'(x) = 2x \cos(x^2)$

Graph for $f(x)$

Graph for $f'(x)$

Q1. Can $f'(x)$ consistently show bigger or more frequent oscillations than $f(x)$? Say, if $f(x)$ is stuck between bounds, could $f'(x)$ shoot off unbounded? What’s the rule here? Also could you provide me with more than one examples?

Q2. Do such functions have special names?

Any answers or comments will be much appreciated!

Are you talking about the behavior as $x \to 0$ or as $x \to \pm \infty$? Because for large $x$ you already gave the example of $f(x) := \sin(x^2)$ which is bounded, but whose derivative is unbounded as $x \to \pm \infty$. — cs89, Apr 01 '25 at 11:15
Basically I am asking which types of functions will always exhibit this kind of behaviour — Random Math Enthusiast, Apr 01 '25 at 11:17
Depending on exactly how you define "oscillating", the functions at is an infinitely differentiable function increasing on an interval if it is increasing $\text{}$at a point$\text{}$? may be of interest. — Dave L. Renfro, Apr 01 '25 at 12:38

score 1 · Accepted Answer · answered Apr 01 '25 at 12:45

Osciallatory functions can be representes as Fourier series in an intervall if some smoothness and norm conditions are met.

See e.g. a Fourier series with random coefficients, becoming small with $1/k^2$. Any differentiaton multiplies each components by its k value

    f = Function @@ {x, 
          Sum[RandomReal[{-1, 1}] 1/(1 + k^2) Cos[k x], {k, 0, 88, 2}]}

and you see

    Plot[{f[x], f'[x] , 1 + 1/6! f'''[x]}, {x, 0, 2 \[Pi]}]

Can a Function’s Derivative Oscillate More Than the Function Itself?

1 Answers1