TLDR: What is the closed-form (if it exists, of course) of the trigonometric summation of the following expression: $$ \sum_{m=1}^{n-1} \csc \left( \frac{(m)\pi}{n} \right) $$
[SOLVED.]
Please go through the post to check whether there are any conceptual errors in my analysis (if needed please request a more detailed derivation and I'll be happy to provide it). This might end up as a check-my-work type of question, and I'm aware of this being a possible duplicate as well, but I just want to know whether the underlying principles agree with my analysis. And if anyone is able to help with the plotting of the graph as well, it would greatly be appreciated.
So here's the deal: I’ve been working on an electrostatics problem, as a personal project, that involves a regular n-gon, and at each vertex, a charge of $+q\,$ is placed (Yes, this is indeed on the Math SE; scroll to the bottom for a justification). My goal is to determine the net electrostatic repulsion force on a charge at one of the vertices, say $F_1\,$, and compare this with the force on a charge at one end of a 1-unit line segment due to another charge at the other end of the segment, say $F_{line}$.
Now, assume the following: $F_1 = k \cdot F_{line}$
This is the base of my problem. Now, the task I have undertaken: Plot a graph between $k$ and $n$ (number of vertices) for a unit side length. However, I appear to be getting stuck at a particularly difficult trigonometric summation in the process.
Problem Setup:
Consider a regular n-gon with side length 1 unit, and suppose a charge $+q$ is placed at each vertex $j_1, j_2, j_3, \dots,j_n$. The electrostatic repulsion force between any two charges is given by Coulomb’s law. The main challenge is to compute the net force $F_1\,$ experienced by the charge at any one vertex, say at vertex $j_1$.
Since this is the math SE, let's provide some basic idea into the physics part. Coulomb's law (well, a particular case of it) states that "the force $F$ on a charge $q_1$ by another charge $q_2$, separated by a distance $r$ from it, is given by":
$$ F = k_e \,\frac {q_1 \cdot q_2 }{r^2}\;,\;where\;k_e\;is\;a\;constant. $$ Thus, $$ F_{line} = k_e \, \frac {q^2}{1^2} = k_e \cdot q^2 $$
The value of $k_e$ is approximately $9 \times 10^9$, although this is irrelevant to the problem as it turns out. I placed the n-gon on a cartesian plane, with vertex $j_1$ at $(R,0)$. Thus, the net force $F_1$ arises from the vector sum of forces acting on $j_1$ from all other charges in the polygon. I used vector addition and basic Coulomb’s law to compute the force as follows.
My Approach:
The central angle (the angle subtended by vertex 1 and any other vertex measured from the center of the polygon) is $\frac{2\pi}{n}$. Each pair of charges has a unique (increasing) angle. The net force on $j_1$ is the vector sum of all forces acting on it:
$F_1 = F_{12} + F_{13} + F_{14} + \dots + F_{1n}$
i.e. $\dots$ $$ F_1 = \sum_{j=2}^{n} F_{1j} $$
where $F_{1j}$ is the force on 1 due to j as given by Coulomb's law.
After some thinking, one can see that the key geometric idea here is that, by symmetry, the vertical components of a force and its opposite on the other side cancel. After some rather painful algebra and geometry, it turns out that the horizontal (x‑axis) component sums to give:
$$ F_1 = k_e \,\frac {q^2}{4R^2}\cdot \sum_{j=2}^{n} \csc ^2 \left( \frac{(j-1)\pi}{n} \right) \sin \left( \frac{(j-1)\pi}{n} \right) $$
where $R$ is the circumradius of the regular n-gon, given for a unit side length by: $$ R = \frac {1}{2 \cdot \sin \left( \frac {\pi}{n} \right)} $$
Now, taking $m=j-1\,$... $$ F_1 = k_e \,\frac {q^2}{4R^2}\cdot \sum_{m=1}^{n-1} \csc \left( \frac{(m)\pi}{n} \right) $$
And this is the elephant in the room (as far as I can see). I tried to use some known trigonometric identities and simplifications, but I couldn’t find a way to express the summation $$ \sum_{m=1}^{n-1} \csc \left( \frac{(m)\pi}{n} \right) $$ in closed-form.
I’ve tried various approaches, including, as a last-ditch effort, asking ChatGPT. Even it kept spewing out random incorrect "results" that did nothing to simplify it. I myself, after some research, couldn’t find a closed-form simplification. I suspect that this sum cannot be simplified in a way that leads to an easily interpretable formula for the force, but I’d like to confirm this with anyone that can offer insight into this.
I’d appreciate any help or suggestions on how to proceed further from this trigonometric summation. Thanks in advance!
PS: This is my first SE question, so please pardon me if I'm inadvertently breaking some rule (or maybe not following some formatting/posting convention, perhaps?) and do let me know.
PPS: Yes, I'm well aware the underlying question is a physics problem. However, the part where I'm getting stuck at is a trigonometric summation, so I kind of hoped the SE maths community might have something to offer more than the physics community :) ... I must also mention that I'm a first-year physics student, and so please forgive my limited mathematical knowledge.
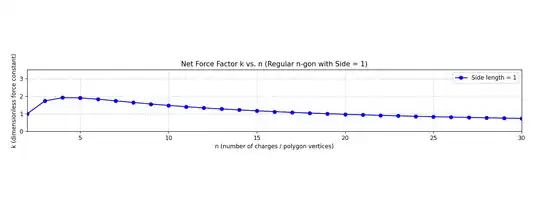
Thank you to the commenters for pointing out related questions! I had gone through them, and, after some tinkering about, I have accomplished my original goal of plotting a k-n graph for an increasing n-gon. Below is the graph for the curious.
Interestingly enough, the graph peaks at n=4, i.e. a square, with a k-value of ($\sqrt 2 + 0.5$)$\,\approx1.914$. Thus, the maximum force of repulsion felt by a charge placed at the vertices of a unit n-gon due to the other charges is a square, at $\,\approx$ 1.914 times that of the the normal electrostatic force of repulsion felt by two like charges placed 1 unit apart.
Also note how, as expected, as $n\to\infty\,$, $k\to0\,$. I will indeed dive deeper into the unexpected result of peaking at n=4, but as of now, my question is answered. Thanks again!