0

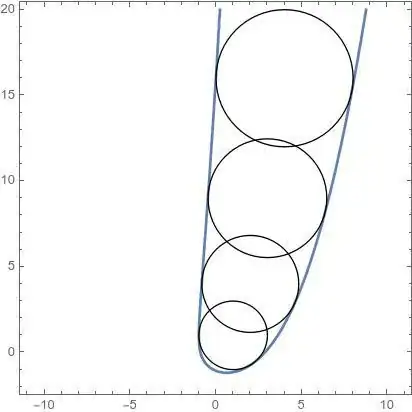
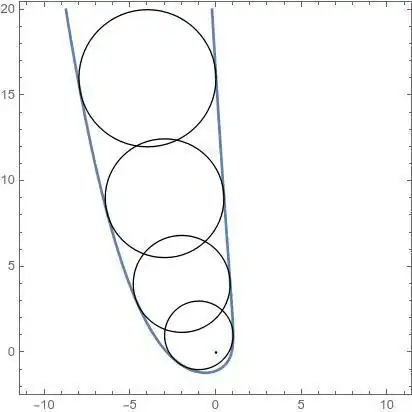
I am trying to determine the envelope of a family of circles defined by: $$\left(x-k\right)^2+\left(y-k^2\right)^2=4\left|k\right|,k\in\mathbb{Z}^*$$ I have searched MSE and found a similar discussion from 12 years ago (Studying the envelope of a family of circles). While that post addressed a rather related problem, my situation involves a slight variation on RHS.

I am quite new to algebraic geometry and I appreciate your patience with my inflexibility. Any insights, suggestions, or references that could help would be greatly appreciated.

Thomas Peng
  • 407

1 Answers1

1

Given the curve $f(x,y,k) = 0$ the envelope can be obtained easily by eliminating $k$ from

$$ \cases{ f(x,y,k)=0\\ \frac{d}{dk}f(x,y,k)=0 } $$

Follows a plot showing in black a set of circles and in blue their envelope.

enter image description here

EDIT

The envelope variety can be obtained with the help of Groebner basis. Follows a MATHEMATICA script which uses that with the command Eliminate.

circk = (x - k)^2 + (y - k^2)^2 - 4 k;
dcirck = D[circk, k];
curve = Eliminate[{circk == 0, dcirck == 0}, k]

$$ 16 x^6+16 x^4 y^2-40 x^4 y+x^4-288 x^3 y-72 x^3-32 x^2 y^3+32 x^2 y^2-290 x^2 y-504 x^2-256 x y^3+96 x y^2+24 x y-868 x+16 y^4-264 y^3+97 y^2+24 y-436=0 $$

The complete set of varieties is obtained considering also

circk = (x + k)^2 + (y - k^2)^2 - 4 k;
dcirck = D[circk, k];
curve = Eliminate[{circk == 0, dcirck == 0}, k]

$$ 16 x^6+16 x^4 y^2-40 x^4 y+x^4+288 x^3 y+72 x^3-32 x^2 y^3+32 x^2 y^2-290 x^2 y-504 x^2+256 x y^3-96 x y^2-24 x y+868 x+16 y^4-264 y^3+97 y^2+24 y-436=0 $$

enter image description here

Cesareo
  • 36,341