2

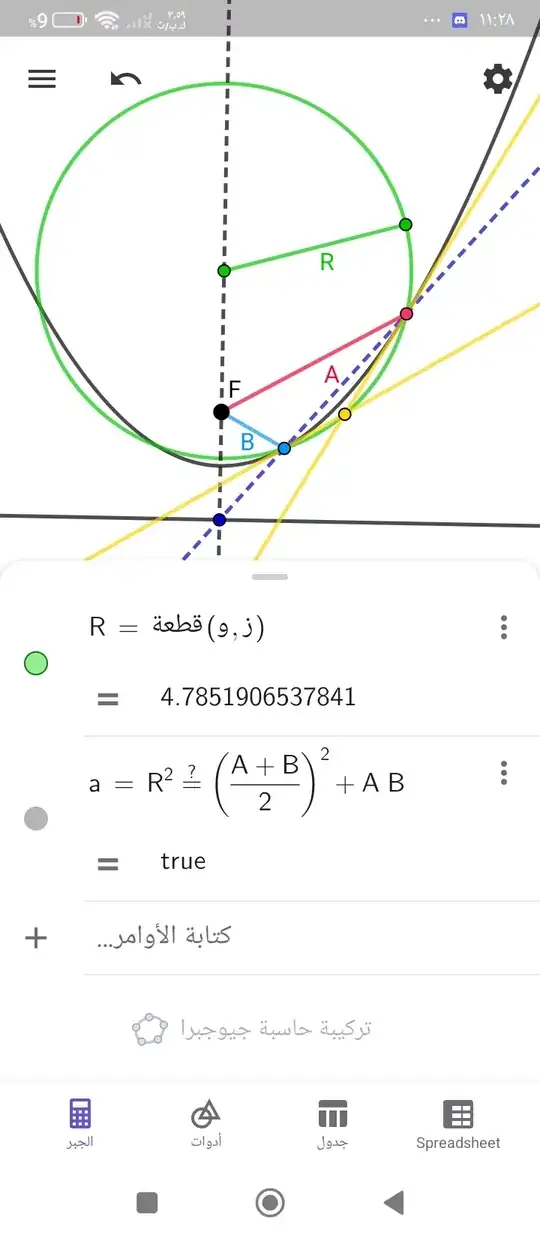
Yesterday, while playing with the GeoGebra app, I discovered a new property of the parabola, but I have not proven it yet. Can anyone help?

If a straight line intersects a parabola at two points and passes through the projection of its focus onto its directrix, then the square of the radius of the circle passing through these two points and the intersection point of the tangents to the parabola at them is equal to the square of the arithmetic mean of the distances from the focus to these two points plus the square of the geometric mean of the lengths of these two distances.

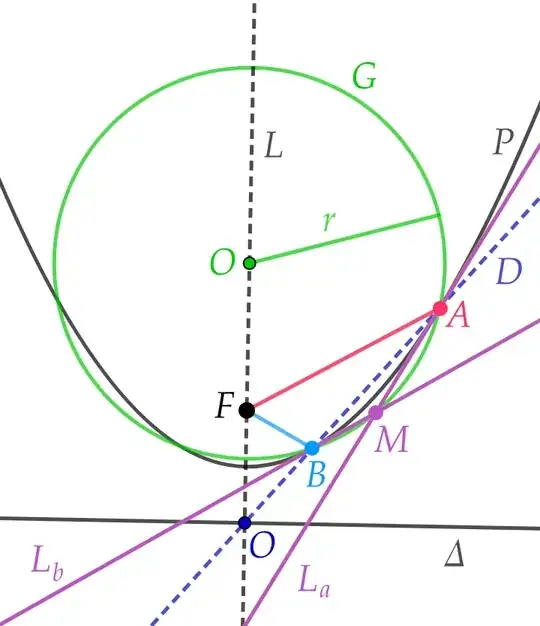
enter image description here

Given: Let $P$ be a parabola with focus $F$, directrix $\Delta$, and axis of symmetry $L$. Let $L \cap \Delta = O$, and let $D$ be a line passing through $O$ such that $P \cap D = (A,B)$. Let $(L_a)$ and $(L_b)$ be the tangents to $P$ at $A$ and $B$, respectively, and let $(L_a) \cap (L_b) = M$. Let $G$ be the circle passing through the points $A, B, M$, and let its radius be $r$.

To Prove: $ r^2 = \left(\frac{\overline{AF} + \overline{BF}}{2} \right)^2 + \overline{AF} \cdot \overline{BF} $

I prefer a proof using Euclidean geometry, which is why I am posting this question.

It is easy to observe that: $ \overline{AF} \times \overline{BF} = \overline{MF}^2 $ since $ \triangle FBM \sim \triangle FMA $.

However, we need to show that: $ \overline{OF}^2 = \left(\frac{\overline{AF} + \overline{BF}}{2} \right)^2 $

Then the theorem follows from the Pythagorean theorem. How can we prove this?

enter image description here

Also, is this property already known? If so, please indicate a source that mentions it, thank you.

زكريا حسناوي
  • 4,060
  • 7
  • 25
  • This question is related to this property https://math.stackexchange.com/a/4942683/958919 – زكريا حسناوي Mar 21 '25 at 03:10
  • 1
    FYI: For a general conic with eccentricity $e$, defining $a:=|AF|$ and $b:=|BF|$ (and with line $AB$ still containing the point where the major axis crosses a directrix, but with the circle's center not necessarily on the axis), the result becomes gains a messy correction term $$r^2 = \frac14 e^2(4ab+e^2(a+b)^2)\cdot\left(1-\frac{(1-e^2)^2(a + b)^2}{4;(a(1+e)-b(1-e));(a(1-e)-b(1+e))}\right)$$ (Found by coordinate bashing.) Even in this general case, $FM$ is perpendicular to the axis and bisects $\angle AFB$. – Blue Mar 21 '25 at 07:20
  • 1
    FYI (addendum): If $p$ is the length of the latus rectum, and thus also the harmonic mean of $a$ and $b$ in such configurations ($p=2ab/(a+b)$), we can write $$\begin{align} r^2 &= \frac14e^2(4ab+e^2(a+b)^2)\cdot\left(1-\frac{1}{k}\right) \ k &= p^2 \left(\frac1{a(1 + e)} - \frac1{b(1-e)}\right) \left(\frac1{a(1 - e)} - \frac1{b(1+e)}\right)\end{align}$$ So, the correction term is still a bit messy, but messy in a more interesting way. – Blue Mar 21 '25 at 07:34

1 Answers1

3

Given that chord $AB$ passes through $D$ on the directrix, and $D$ is collinear with the parabola's axis, so that the intersection point $M$ of tangents at $A$, $B$ always lies on the perpendicular to the axis at $F$:

Draw a circle with radius $FB$, crossing $AF$ at $L$. By symmetry, $AF$ extended passes through the intersection of circle $OM$ with the parabola at $K$, and $$FK=FB$$Next draw a circle with radius $FO$, extend $OD$ to $N$, $AK$ to $R$, and draw a perpendicular to $MF$ at $M$, crossing $AK$ at $H$.

If as OP notes $AF\times BF=MF^2$, then also $$AF\times LF=MF^2$$and $FM$ is tangent to the circle through $A$, $L$, $M$, whose center thus lies on $MH$ or its extension. (Cf. Euclid, Elements III, 36-37).

circle & parabola

Further, since $MV$ is tangent to the parabola at $A$, then drawing $AU$ parallel to $MH$ and the axis,$$\angle VAU=\angle FAM=\angle AMH$$Therefore, $AH=MH$, $H$ is the center of circle $ALM$, and$$HA=HL=KR$$

And since$$AF+BF=AK=HR=ON=2OF$$then$$OF=\frac{AF+BF}{2}$$

Edward Porcella
  • 5,178