3

There are $3^{14} = 4782969$ cities on the magical planet π. Each city has a teleportation station, and the distance between any two stations is not equal. If all the cities send diplomatic ambassadors from this station to the nearest station at the same time, how many teleportation rooms should be prepared for the station that receives the largest number of people?

Is this nearest neighbor graph? Below is my attempt, assuming planet π is $[0,1]^2$.

What if planet π is $[0,1]^3$, $S^1$, $S^2$?

Clear["Global`*"];

(* Define the function - no changes needed here *)
monteCarloNearestNeighbor[n_, trials_] := 
  Module[{results}, 
   results = Table[
     With[{points = RandomReal[1, {n, 2}]}, 
      Max[Map[Identity, VertexDegree[NearestNeighborGraph[points, DirectedEdges -> True]]]]], 
     {trials}];
   <|"Mean" -> Mean[results], "StandardDeviation" -> StandardDeviation[results], 
    "MaxObserved" -> Max[results], "MinObserved" -> Min[results]|>];


(* Define parameters )
trials = 5000;   ( number of Monte Carlo trials )
nValues = Range[100, 300, 50];  ( range of n values to test *)


(* Launch kernels if not already launched )
Print["$KernelCount=", $KernelCount]; ( Shows number of available parallel kernels )
LaunchKernels[Max[$KernelCount - 5, 1]]; ( Ensure at least 1 kernel, adjust if needed *)


(* Parallel computation with progress monitoring )
SetSharedVariable[data];
data = ParallelTable[
   With[{result = monteCarloNearestNeighbor[n, trials][["Mean"]]}, {n, result}], 
   {n, nValues}, 
   Method -> "CoarsestGrained", ( Optimizes task distribution )
   DistributedContexts -> Automatic ( Ensures function availability *)];


(* Create the plot *)
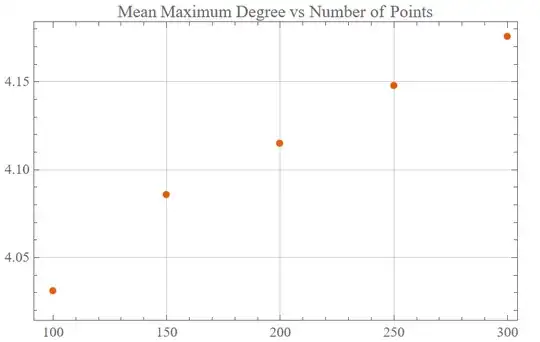
plot = ListPlot[data, 
   PlotLabel -> "Mean Maximum Degree vs Number of Points", 
   AxesLabel -> {"n (Number of Points)", "Mean Max Degree"}, 
   PlotStyle -> PointSize[Medium], PlotRange -> All, 
   GridLines -> Automatic, PlotTheme -> "Scientific"];


(* Show the plot *)
Show[plot]

enter image description here

138 Aspen
  • 1
  • I found this question at Zhihu, A Chinese Q&A site like Quora. – 138 Aspen Mar 14 '25 at 05:54
  • Hi , from your question "If all the cities send diplomatic ambassadors from this station to the nearest station at the same time, how many teleportation rooms should be prepared for the station that receives the largest number of people?"
    1. How many ambassadors from each city ?
    2. What is a teleportation room in the context of the question?
     – vishalnaakar25 Mar 14 '25 at 06:06
  • @vishalnaakar25  One ambassadors from each city. Each person received needs a teleportation room. – 138 Aspen Mar 14 '25 at 06:08
  • It is not clear in your question what you need for; as expected number or a lower/higher bound. A lower bound is 2 and you cant expect better: imagine the city grouped as pairs where pairs are close. because there's an even number of cities we need to group three of them together. An expected number sounds not that trivial to calculate and seem related to what you actually did. An higher bound does not seem trivial either although I would assume something not "too high" is to be expected, and the result might vary depending on the space you consider (see next comment) – Qise Apr 04 '25 at 08:00
  • For instance with $[0,1]^2$ I think it's possible that 5 or 6 is an upper bound: imagine a regular pentagon and its center as cities. with nodes 6 that does not work anymore as a regular hexagon is made of 6 equilateral triangles. So I guess it is up to you to decide if a regular hexagon is a valid configuration or not. If you consider higher dimensions or even $S^1, S^2$ etc. I figure looking into that regular polygons/polyhedrons and respective distance to the centers is a good start – Qise Apr 04 '25 at 08:05

0 Answers0