Why Definite Integral is sometimes not equal to difference of indefinite integral evaluated at bounds?

Question

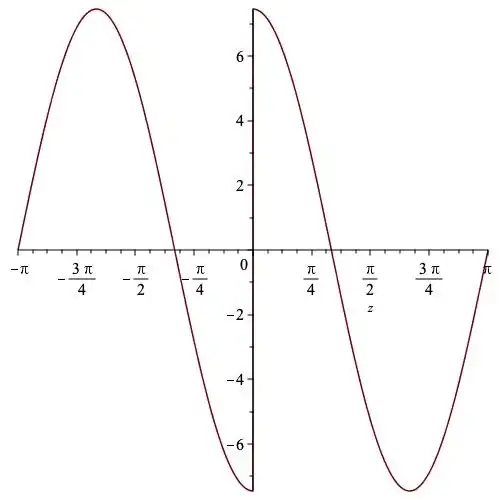
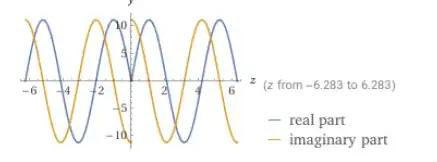
I'm trying to calculate the definite integral: $$\int_{-\pi}^{\pi} (-5\ e^{iz})^{\frac{3}{2}} e^{-inz} dz $$

The indefinite integral without the constant of integration is:

$$ \frac {10 i\sqrt {5}\sqrt {-e^{i z}} e^{-i (n - 1) z}} {2 n - 3} $$

The difference of the indefinite integral evaluated at the bounds $\{-\pi,\pi\}$ is

$$ \frac{10 i \sqrt{5} e^{-i \pi (n-1)}}{2 n-3}-\frac{10 i \sqrt{5} e^{i \pi (n-1)}}{2 n-3} $$

If I substitute $n$ for a positive integer this difference evaluates to $0$

Also the difference can be simplified to

$$ \frac{10 i \sqrt{5} e^{-i \pi (n-1)}}{2 n-3}-\frac{10 i \sqrt{5} e^{i \pi (n-1)}}{2 n-3} = \frac{20 \sqrt{5} \sin (\pi n)}{2 n-3} $$

If I ask Mathematica to compute the definite integral

Integrate[E^(-I*n*z)*((-5*E^(I*z))^(3/2)), {z, -Pi, Pi}],

it produces:

$$ \frac{20 \sqrt{5} (\sin (\pi n)+1)}{2 n-3} $$

I'm using this to generate a Fourier series of $$ {(-5\ e^{i\ z})}^{\frac{3}{2}} $$

Using the definite integral that Mathematica produces, I am able to produce a Fourier series that converges correctly. But using the definite integral obtained from taking the difference of the indefinite integral at the bounds, I can't generate a correctly converging fourier series since $n$ substituted for positive integers always causes the expression to equal $0$

So what I'm wondering is how did Mathematica generate the correct definite integral?, why doesn't computing the definite integral the typical analytic way work?, and is there a way to calculate the correct definite integral using the indefinite integral in this case?

Answer 1

In order for the definite integral to equal the difference of the indefinite integral at the two endpoints, there are some hypotheses to check. For example, that indefinite integral must be continuous on the interval. That fails for your indefinite integral....

Example.
In $$ F_n(z) := \frac {10 i\sqrt {5}\sqrt {-e^{i z}} e^{-i (n - 1) z}} {2 n - 3} $$ let's take $n=3$. $$ F_3(z) = {\frac {10\,i}{3}}\sqrt {5}\sqrt {-{{\rm e}^{iz}}}{{\rm e}^{-2\,iz}} $$ Here is the real part $\operatorname{Re}(F_3(z))$:

It has a jump at the origin. To get a continuous antiderivative, you have to adjust the "$+C$" when you pass $0$:

Answer 2

Part of the problem here is that your integrand is discontinuous. For example, taking $n = 3$ and taking the usual branches of the complex principal square root, the graph of $(-5\ e^{iz})^{3/2} e^{-inz}$ looks like this (from Wolfram Alpha):

There is an obvious discontinuity at zero.

Many of the elementary calculus texts you might look into for the Fundamental Theorem won't tell you what to do in a case like this, because they only cover the case of an integrand that is continuous on its entire domain. Those references don't even define your integral. But your kind of integral is addressed in some of the answers to Continuity & differentiability of an improper integral of discontinuous function and Is an integral always continuous? The conclusion is that if the integral is defined in any of the ways mentioned in those answers, it is continuous.

Your method of integration finds a local antiderivative at (almost) every point of the domain, but the formula that it gives you is a formula for a function that is discontinuous at zero. In order to be able to use the Fundamental Theorem the way you want to, you need a single continuous integral over the entire interval $[-\pi,\pi].$ The piecewise nature of $\sqrt{e^{iz}}$ got you into this mess and the simplest way out is a piecewise "adjustment" of the antiderivative to obtain a continuous indefinite integral.

Note that even after this adjustment, you still have a constant of integration, ${}+C,$ to apply to the indefinite integral.