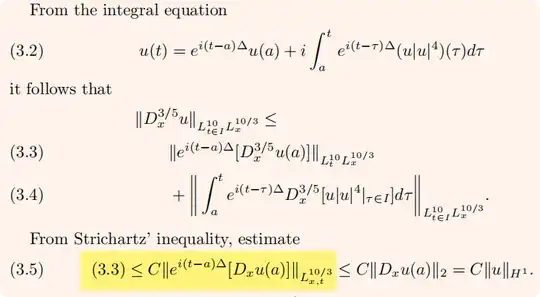2

enter image description here

In Bourgain's 1999 jams paper, when he proved the concentration property, he say that $(3.3)\leq C\|e^{i(t-a)\Delta}[D_x u(a)]\|_{L^{10/3}_{x,t}}$, Why? I have struggled a long time on this issue but still don't know how to do, is it easy to see?

By Strichartz estimates, I just know the second inequality in (3.5): $ \| e^{i(t-a)\Delta} [D_x u(a)] \|_{L_{x,t}^{10/3}}\lesssim\|Du(a)\|_{L^2}$ because in $\mathbb{R}^3$, we have admissible pair $\frac{1}{q}=\sigma(\frac{1}{2}-\frac{1}{r})$ where $2<q,r\leq\infty$ and $\sigma=\frac{3}{2}$. $ L_{x,t}^{10/3} $ correspondents to $q=r=\frac{10}{3}$ we have $\frac{3}{2}(\frac{1}{2}-\frac{1}{10/3})=\frac{3}{2}(\frac{5}{10}-\frac{3}{10})=\frac{3}{2}\times\frac{2}{10}=\frac{3}{10}$.

Any hints are wellcome!!!

Mittens
  • 46,352
monotone operator
  • 836

1 Answers1

2

$$(3.3)=\|D_t^{-1/5}e^{i(t-a)\Delta}D_xu(a)\|_{L_t^{10}L_x^{10/3}}\\ =\|\|e^{i(t-a)\Delta}D_xu(a)\|_{L_x^{10/3}}\|_{\dot H_{10/3,t}^{-1/5}}\\ \le C\|e^{i(t-a)\Delta}D_xu(a)\|_{L_t^{10/3}L_x^{10/3}},$$ where for the last inequality we use the embedding $$\dot H_p^s \hookrightarrow \dot H_q^r, \ \ \ \frac 1p-\frac 1r=s-r>0$$ and the equivalence $$\dot H_p^0=L_p, \ \ \ 1<p<\infty.$$

Vegetable chicken
  • 131
  • thank you very very much! I have a question that where the $D^{-1/5}{t}$ come from? does it come from $D{t}\sim D_{x}^{2}$? – monotone operator May 23 '25 at 08:52
  • For $\alpha\in \mathbb N,$ it's easy to see $D_t^{\alpha}e^{it\Delta}=e^{it\Delta}(i\Delta)^{\alpha}.$ For $\alpha \notin \mathbb N,$ we have the same conclusion since $\frac{d^\alpha}{dx^\alpha}e^x=x^\alpha e^x.$ For this, see Theorem 2.1 in https://doiserbia.nb.rs/img/doi/0353-8893/2002/0353-88930213077T.pdf – Vegetable chicken May 24 '25 at 01:48
  • thank you for your expanation, I think it is very intuitive! but in this case, what we deal with is $e^{it\Delta}$ which is an operator not $e^{x}$, a function, can we still use the fractional derivative for operator(we even know that $\Delta$ is unbounded) – monotone operator May 25 '25 at 12:05
  • Yes we can. It's just a functional calculus. The only thing we need is that $u$ belongs in the domain of $e^{it\Delta}D_x^{\frac 35}.$ However, it has been shown by the Strichartz inequality. – Vegetable chicken May 26 '25 at 05:14