8

I've been interested in the Basel problem and its famous solution $$ \sum_{n=1}^{\infty}{\frac{1}{n^2}} = \frac{\pi^2}{6}. $$

Recently I saw this video along with a comment (highlighted from the link) stating

Cool fact: Euler actually approximated the sum to 16 decimal places and GUESSED that it was pi^2/6 before rigorously proving it

I know that Euler (and other mathematicians, related post) had approximated the sum by transforming it into a sum that converged quicker: $$ \sum_{n=1}^{\infty}\frac{1}{n^2} = \sum_{n=1}^{\infty}\frac{1}{2^n n^2} + (\ln2)^2, $$ but I never knew of the second part nor could I find any source that supports this comment. The trusty source ethanyap8680 is likely mixing/making things up.

So, is it even possible for Euler, or anyone for that matter, to guess the sum to be $\frac{\pi^2}{6}$ from the approximation $1.6449340668482264$? The only way I could see it is if they assumed there was some connection to $\pi$ along with some constant, specifically $$ 1.6449340668482264 \approx c\pi^k $$

A rural reader
  • 3,004
FishDrowned
  • 1,019
  • 4
    I think you would do better to post this on hsm.stackexchange.com. – Rob Arthan Mar 02 '25 at 21:51
  • I thought of that but my preliminary question of "did he do this" seems to be no seeing as there are no explicit sources other than this one comment. I'm more curious on how one might have done this. – FishDrowned Mar 02 '25 at 21:53
  • 6
    There was a time when mathematicians did a lot more computation and numerics. I, having taught trigonometry, immediately recognize $1.414213{\dots}$, $0.7071067{\dots}$, $0.8660254{\dots}$, $1.154700{\dots}$ and several small multiples of $3.14159{\dots}$, $0.785398{\dots}$, and $0.523598{\dots}$. Teaching calculus permanently etched $2.718281828{\dots}$, $0.367879{\dots}$, and $0.268941{\dots}$ permanently into my memory. (Together with the reminder that we asked for exact answers, not (calculator vomit) approximations.) Q.v. https://en.wikipedia.org/wiki/Inverse_Symbolic_Calculator – Eric Towers Mar 02 '25 at 21:55
  • Also, generically, it's much easier to find a proof that a limit has a particular value if you already have some means of guessing that value. In "Advanced Calculus", students write such proofs, but occasionally have to be reminded that all their previously acquired sequence/series knowledge is still available for finding the values of the limits they attempt. – Eric Towers Mar 02 '25 at 21:58
  • OK. So you are looking for wild guesses $\ddot{\smile}$: I think it is very likely that Euler would have tabulated values of expressions like $\pi^m/n$ and would have spotted that the Basel sum looked close to $\pi^2/6$ (along the lines of @EricTowers's comments) . You could see if the HSM stack exchange people have any light to shed on the relevant numerical data that Euler accumulated. – Rob Arthan Mar 02 '25 at 22:10
  • 1
    While not itself a source, a more prominent instance of this claim is from volume 1 of Polya's "Mathematics and Plausible Reasoning": "Yet Euler had reasons to trust his discovery. First of all, the numerical value for the sum of the series which he has computed before, agreed to the last place with $\pi^2/6$." Polya further notes that Euler's method further gave the sum of reciprocal fourth powers, and again found numerical agreement (page 20). – Semiclassical Mar 02 '25 at 22:20
  • @Semiclassical I believe this is about his discovery of $\frac{\sin{x}}{x}$ as a polynomial via the roots rather than approximating the value and "guessing" the exact value to be $\frac{\pi^2}{6}$ (prior to the proof). Useful source though, thank you. – FishDrowned Mar 02 '25 at 22:27
  • 5
    This is the original paper / book (where he found $\approx 1.644934$) (solution at page $104$). I don't see any mentioning of $\pi^2/6$. This is the paper / book (solution at page $133$) where he proved it. – The Art Of Repetition Mar 02 '25 at 22:42
  • IMO the assumption that the constant would be related to $\pi$ is at least somewhat reasonable, given that they knew of the similar Leibniz formula for $\pi/4$. That being said, I can't find concrete evidence of this guessing anywhere, though I'm certain it's true. The confusion might stem from this quote from the Wikipedia article: "Euler computed this sum to 20 decimal places with only a few terms... This probably convinced him that the sum equals ⁠$π^2/6$⁠, which he proved in the same year." – mediocrevegetable1 Mar 03 '25 at 03:39
  • 3
    Notably, the Wikipedia quote contains a source, but the source itself (from a skim, at least) doesn't say anywhere that Euler himself probably used the approximation to guess a value. The closest thing I found is this: "They were likely trying to guess the exact value of the sum, hoping to recognize that their approximations hinted something familiar, perhaps involving $\pi$, like Leibniz’s series, which had summed to $\pi/4$." The quote itself doesn't have a source in this paper either, so maybe it's just a bad game of telephone? – mediocrevegetable1 Mar 03 '25 at 03:44
  • Note: I asked this question on the History of Science and Mathematics stack exchange and received an answer. – FishDrowned Mar 27 '25 at 14:03
  • 5
    I’m voting to close this question because it was crossposted in https://hsm.stackexchange.com/questions/18364/did-euler-guess-the-basel-problem-s-solution-to-be-frac-pi26, where it received an accepted answer. – Gonçalo Apr 28 '25 at 22:08

1 Answers1

-1

The approximation

$$ L = \int_{x=1}^\infty \frac{1}{x^2} = \left[ -\frac{1}{x}\right]^\infty_1 = 1$$

actually undercounts the true area of

$$ \sum_{x=1}^\infty \frac{1}{n^2}$$

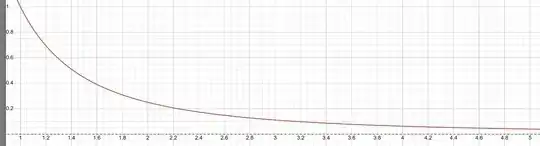
enter image description here

Adding the sum of all the triangular deficits

$$ T = \frac{f(1)-f(2)}{2} + \frac{f(2)-f(3)}{2} + \frac{f(3)-f(4)}{2} + ...= \frac{f(1)}{2}= \frac{1}{2}$$

so that

$$ \sum_{x=1}^\infty \frac{1}{n^2} \approx L + T = 1 + \frac{1}{2} = 1.5$$

which still undercounts the true area by a small crescent shaped summation.

E.g. area of the first crescent between $x=1$ and $x=2$ is area of the trapezoid minus area under the integral

$$ A_1 = \frac{1}{2}\left(\frac{1}{1^2} + \frac{1}{2^2}\right) - \left(\frac{1}{1} -\frac{1}{2} \right) = \frac{5}{8} - \frac{1}{2} = \frac{1}{8}$$

In general

$$A_n = \frac{1}{2}\left(\frac{1}{n^2} + \frac{1}{(n+1)^2}\right) - \left( \frac{1}{n}-\frac{1}{n+1} \right) = \frac{1}{2n^2(n+1)^2}$$

Therefore the infinite sum of all cresents:

$$A = A_1 + A_2 + A_3 + ...$$

exactly accounts for the remaining area deficit.

Hence

$$\sum_1^\infty \frac{1}{n^2}= L + T + A$$ $$= 1 + \frac{1}{2} + \sum_{i=1}^\infty \frac{1}{2n^2(n+1)^2}$$

which converges termwise as $O(\frac{1}{n^4})$ faster than the original $O(\frac{1}{n^2})$.

Further convergence acceleration may be achieved by splitting

$$\sum_{i=1}^\infty \frac{1}{2n^2(n+1)^2}$$

into easily calculated boundary terms $+$ an even faster converging infinite sum.

Euler used the same general method to carve away successive boundary terms using integration by parts. Starting with

$$A_1 = \frac{f(0)+f(1)}{2} - \int_0^1 \color{blue}{1} \cdot \color{green}{f(x)} dx$$

Integrating by parts using $u = \color{green}{f(x)}$ and $dv = \color{blue}{1 \cdot dx}$,

$$A_1 = \frac{f(0)+f(1)}{2} - \left[f(x)(x+c)\right]_0^1 + \int_0^1 (x+c) f^1(x) dx$$

Since $c$ may take on any value, choosing $c=-\frac{1}{2}$ gives

$$A_1 = \frac{f(0)+f(1)}{2} - \frac{f(1)+f(0)}{2} + \int_0^1 \left(x-\frac{1}{2}\right) f^1(x) dx$$

$$= \left[f^1(x) \left(\frac{x^2}{2}-\frac{x}{2}+ c\right)\right]_0^1 - \int_0^1\left(\frac{x^2}{2}-\frac{x}{2}+ c\right)f^2(x)dx$$

Choosing $c=\frac{1}{12}$,

$$=\frac{f^1(1)-f^1(0)}{12} - \int_0^1\left(\frac{x^2}{2}-\frac{x}{2}+ \frac{1}{12}\right) f^2(x)dx$$

$$=\frac{f^1(1)-f^1(0)}{12} - \left[f^2(x)\left(\frac{x^3}{6}-\frac{x^2}{4}+ \frac{x}{12}+c\right)\right]_0^1 + \int_0^1 \left(\frac{x^3}{6}-\frac{x^2}{4}+ \frac{x}{12}+c\right) f^3(x)dx$$

Choosing $c=0$,

$$=\frac{f^1(1)-f^1(0)}{12} + \int_0^1 \left(\frac{x^3}{6}-\frac{x^2}{4}+ \frac{x}{12}\right) f^3(x)dx$$

$$=\frac{f^1(1)-f^1(0)}{12} - \left[f^3(x)\left(\frac{x^4}{24}-\frac{x^3}{12}+ \frac{x^2}{24} + c\right)\right]_0^1 + \int_0^1 \left(\frac{x^4}{24}-\frac{x^3}{12}+ \frac{x^2}{24} + c\right) f^4(x)dx$$

Choosing $c=-\frac{1}{720}$,

$$=\frac{f^1(1)-f^1(0)}{12} - \frac{f^3(1)-f^3(0)}{720} + \int_0^1 \left(\frac{x^4}{24}-\frac{x^3}{12}+ \frac{x^2}{24} + c\right) f^4(x)dx$$

$$\approx \frac{f^1(1)-f^1(0)}{12} - \frac{f^3(1)-f^3(0)}{720}$$

ending the approximation.

Since

$$A_1 \approx \frac{f^1(2)-f^1(1)}{12} - \frac{f^3(2)-f^3(1)}{720}$$

$$A_2 \approx \frac{f^1(3)-f^1(2)}{12} - \frac{f^3(3)-f^3(2)}{720}$$

$$A_3 \approx \frac{f^1(4)-f^1(3)}{12} - \frac{f^3(4)-f^3(3)}{720}$$

$$.$$ $$.$$

By telescoping,

$$\sum_i^\infty A_i \approx - \frac{f^1(1)}{12} + \frac{f^3(1)}{720}$$

and since

$$ \left[f^1\left(x\right) = -\frac{2}{x^3} \right]_1 = -2$$

$$ \left[f^3\left(x\right) = -\frac{24}{x^5} \right]_1 = -24$$

Therefore

$$ \sum_1^\infty \frac{1}{n^2} = L + T + A \approx 1 + \frac{1}{2} +\frac{1}{6} -\frac{1}{30} = 1.6 \dot 3 $$

James
  • 922
  • 7
    Does this answer the question? – coiso Apr 28 '25 at 22:37
  • 1
    @coiso thank you for the feedback. Euler carved away successive boundary terms by choosing clever integration constants when integrating by parts, instead of splitting boundary terms directly from the discrete sum. I will try to append Euler's method using integration by parts. – James Apr 29 '25 at 00:02
  • 7
    This does not address the question, which is whether Euler guessed the value just from the decimal expansion or not. Any answer would not be mathematical but historical – Bruno Andrades Apr 29 '25 at 00:45
  • 1
    As coiso pointed out, I'm not looking for the approximation. I'm looking for the connection between the approximation and $\frac{\pi^2}{6}$ intuitively without knowing the answer. – FishDrowned Apr 30 '25 at 01:51
  • @FishDrowned Euler did the approximation before realizing it, so I think any mathematician of his caliber would have strongly suspected that if a number is 17 digits to same as the digit expansion of $\frac{\pi^2}{6}$, it is probably the same thing? :) – James Apr 30 '25 at 01:59
  • @James When I see 1.68249909, I don't immediately realize that since it's the same digit expansion as $\frac{\pi^{\sqrt{2}}}{3}$, that it is the same. The point is that $\frac{\pi^2}{6}$ is so unorthodox, it doesn't make intuitive sense to immediately see that its the answer from the decimal expansion 1.64493407 . – FishDrowned Apr 30 '25 at 12:57
  • @FishDrowned yes, I think you are right it is numerology to some extent. I think in this case though finding a "simple" number like $\frac{\pi^2}{6}$ that is 17 digits the same as $1.6449340668482264$ is quite challenging, plus the fact that Euler could have calculated this value to 50 or 500 decimal places and he would have found that his 50 or 500 digits approximation agree exactly with $\frac{\pi^2}{6}$ as well? – James Apr 30 '25 at 19:17