What is the Fiedler vector if the second smallest eigenvalue of the Laplacian matrix is degenerate?

Question

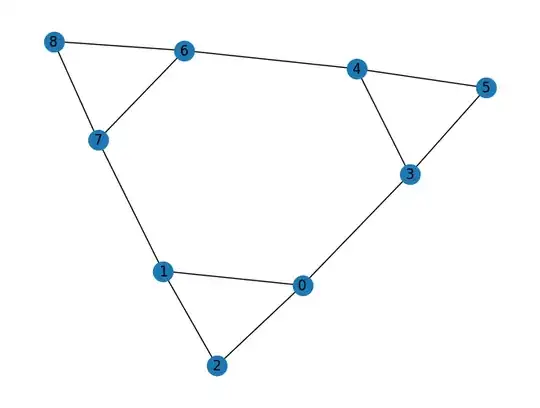
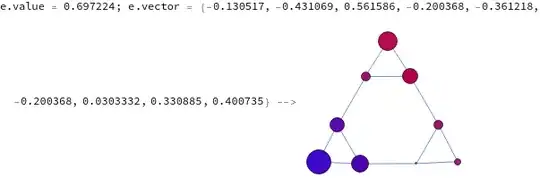
The Fiedler vector is defined as the eigenvector corresponding to the second smallest eigenvalue of a Laplacian matrix. However, what if the second smallest eigenvalue is degenerate (for example, the second and third smallest eigenvalues are equal)? Which of the two eigenvectors corresponds to the Fiedler vector?

For example, consider the graph:

This graph has spectrum:

[-2.22044605e-16, 2.77930869e-01, 2.77930869e-01, 1.12993595e+00, 1.12993595e+00,  1.33333333e+00,  1.59213318e+00,  1.59213318e+00, 1.66666667e+00]

Thus, one can see that the second smallest value is degenerate, while the graph is connected.

Yes, one can write an example where it is a connected graph and the spectrum is degenerate for the second smallest eigenvalue. I will add an example — Zonova, Mar 02 '25 at 13:13
@Zonova, this means you have more than 1 solution to whatever you want the Fiedler vector to do for you; if this is about a partition of the graph (as per https://en.wikipedia.org/wiki/Algebraic_connectivity) having a degenerate eigenvalue, means that you have more than 1 'Fiedler' partition (in this case apparently following the graph's symmetry). What can be tricky in such a case is to pick the correct linear combination of eigenvectors to actually read off the relevant partition... — Michael T, Mar 04 '25 at 17:44

Michael T · Answer 1 · 2025-03-11T14:21:39.647

This means you have more than 1 solution to whatever you want the Fiedler vector to do for you.

If this is about a partition of the graph (as per en.wikipedia.org/wiki/Algebraic_connectivity), having a degenerate eigenvalue, means that you have more than $1$ 'Fiedler' partition (in your example apparently following the graph's symmetries).

Of course, in such a case you can make a choice of 'the' eigenvector as a linear combination of the $2$. This should reflect different possible partitions or may reflect the need to identify the special linear combinations that make most sense in the construction...

Below $2$ examples for your graph - seems to me that you can choose $4$ vertices positive (or $1$ of those $0$)