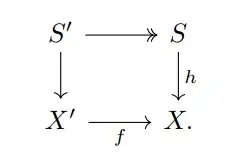0

(In an abelian category $\mathcal A$) Let $X' \xrightarrow{f} X \xrightarrow{g} X''$ be a complex, then this complex is exact if and only if for any morphism $S \xrightarrow{h} X$, satisfying $gh = 0$, there exist morphisms $S' \rightarrow X'$ and $S' \twoheadrightarrow S$ making the following diagram commute: This diagram commutes

This is a lemma in the book of Li Wenwei, and I have some questions about the proof in the book.

The book says that for "$\Rightarrow$": First, both $f$ and $h$ factor through $\ker(g)$. Thus, we take $S' := S \times_{\ker(g)} X'$, and let $S' \to S$ and $S' \to X'$ be the natural morphisms of the fiber product. Exactness implies $X' \twoheadrightarrow \ker(g)$, hence Proposition 2.1.6 implies that $S' \to S$ is also surjective.

My questions:

(1) Is it true that in an abelian category, fiber product $S\times_{\ker(g)}X'$ always exists?

(2) Why does exactness imply that $S'\to S$ is surjective?

I am beginning learning homological algebra, and I just learned the definition of abelian category. I am reading the lemma in order to learn the proof of the five lemma without using elements. Can someone explain in an elementary way? Many thanks in advance!

Edit:

Proposition 2.1.6: If in an Abelian category $\mathcal{A}$ the diagram is a pullback (or pushout) diagram, and $g$ is epic (or monic), then the diagram is also a pushout (or pullback), and $f$ is epic (or monic).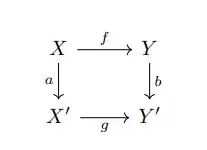The diagram of proposition 2.1.6

And for question (2), I am actually asking why exactness implies $X'\to \ker(g)$ is surjective. I know it's true in for example $R$-mod, but I cannot prove it using the definition of surjectiveness in an abelian category.

shwsq
  • 790
  • 2
  • 16

1 Answers1

1

As I already pointed out in the comments, every abelian category has all finite limits since it has finite products and equalizers, the former by definition and the latter since the equalizer of two maps is the kernel of their difference (see this answer for how/why this is enough).

For point 2, you by definition have a pullback diagram $\require{AMScd}$ $$ \begin{CD} S' @>h>> S \\ @VVV @VVV \\ X' @>>f'> \ker g \end{CD} $$ with $f'$ epic, so the proposition you cite implies that $h$ is epic as desired.

Finally, why is $f'$ epic? Exactness of the given sequence means that the induced map $\operatorname{img} f \to \ker g$ is an isomorphism, so this (hopefully unsurprisingly!) reduces to showing that the map $X' \to \operatorname{img} f$ is epic, for which I commend you to this answer if you do not know it already.

On a sidenote, don't say "surjective." Surjectivity is something that applies to functions between sets, not morphisms in arbitrary categories. Follow your book's example and use "epic" and "epimorphism."

Ben Steffan
  • 8,325