I am reading "Topology Second Edition" by James R. Munkres.
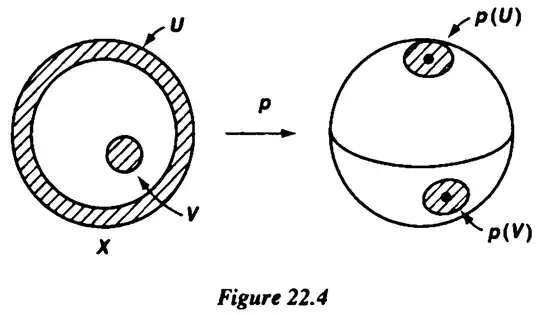
EXAMPLE 4. Let $X$ be the closed unit ball $$\{x\times y|x^2+y^2\leq 1\}$$ in $\mathbb{R}^2$, and let $X^{*}$ be the partition of $X$ consisting of all the one-point sets $\{x\times y\}$ for which $x^2+y^2<1$, along with the set $S^1=\{x\times y|x^2+y^2=1\}$. Typical saturated open sets in $X$ are pictured by the shaded regions in Figure 22.4. One can show $X^{*}$ is homeomorphic with the subspace of $\mathbb{R}^3$ called the unit 2-sphere, defined by $$S^2=\{(x,y,z)|x^2+y^2+z^2=1\}.$$
To show $X^{*}$ is homeomorphic with $S^2$, we need to construct a homeomorphism from $X^{*}$ to $S^2$.
But I think that even constructing a bijection from $X^{*}$ to $ S^2 $ is difficult.
Please tell me about books that deal with this kind of topic.
My attempt:
Let $f:(0,1)\times [0,2\pi)\ni (r,\theta)\mapsto(\pi r,\theta)\in (0,\pi)\times [0,2\pi)$.
Let $g:X^{*}-\{\{0\times 0\},S^1\}\ni\{x\times y\}\mapsto (\sqrt{x^2+y^2},\arg(x\times y))\in (0,1)\times [0,2\pi)$.
Let $l:(0,\pi)\times [0,2\pi)\ni (\theta,\phi)\mapsto(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)\in S^2$
Let $h:X^{*}\to S^2$ be the function such that $h(x)=(l\circ f\circ g)(x)$ if $x\in X^{*}-\{\{0\times 0\},S^1\}$ and $h(\{0\times 0\})=(0,0,1)$ and $h(S^1)=(0,0,-1)$.
Then, $h$ is a bijection from $X^{*}$ to $S^2$.