6

How may I determine the closure of the following set? $$\Omega=\{\cos(n)^n, n\in\mathbb{N}\}$$ It's an exercise from a prestigious oral exam in france but I don't really know how to approach the problem. Variants include density of $\cos(n)$ in $[-1,1]$ and density of $\cos(\ln(n))$ as well, which I managed to handle with some basic intuition (the latter involved the asymptotic behaviour of $\ln$, the former elementary group theory), but I don't really have much of a clue on how to tackle this one. I'vee seen a particular solution to the fact that: $$\overline{\{\cos(\ln(n)), n\in\mathbb{N}^*\}}=[-1,1]$$ By constructing a sequence by hand that converges to any element $y\in[-1,1]$, but it seemed too... artificial. How can I approach this problem by constructing a handmade sequence? And is there a more theoretical way of solving the problem? This is pureley recreational.

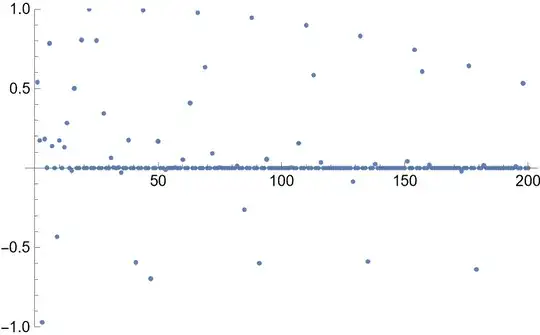
Edit: A list plot of the first 200 entries of the sequence show the unsurprising clustering close to zero.

enter image description here

Jakobian
  • 15,280
J.J.T
  • 1,077
  • perhaps you can use the equivalence that closed <=> complete – Clemens Bartholdy Feb 22 '25 at 12:04
  • 1
    I think this is tougher, and needs more serious number theory, Diophantine approximation in particular (unless I'm missing something trivial). We have examples like $$\cos(22)^{22}\approx0.999139,$$ because $22$ is quite close to $7\pi$. But you need to find integers very close to integer multiples to $\pi$ to show that $1$ is in the closure. After all, raising to a high power will increase the deviation from $1$ (Bernoulli inequality is there though). See the image I added to appreciate this. – Jyrki Lahtonen Feb 22 '25 at 12:49
  • 3
    Related question. – nejimban Feb 22 '25 at 13:15
  • Perhaps related, although normally this result should be proven with relatively elementary real analysis... – J.J.T Feb 22 '25 at 13:21
  • 1
    Well, you mentioned “prestigious oral exam in France”… I'm guessing X-ENS? I am pretty sure that the Diophantine approximation used in the answer I linked appears in the common books for this exam. – nejimban Feb 22 '25 at 13:50
  • Yes, but could this really be the method awaited by the examiners? Keep in mind that the previous two questions were the ones I mentioned in the post, and so to successfully treat the entire exercise one would need to havemore than a considerable amount of extra curricular knowledge. – J.J.T Feb 22 '25 at 13:56
  • X-ENS oral exam questions are notoriously difficult, and from my personal experience (15 years ago…), you need not solve the exercise entirely to pass the exam. I would be surprised to see a much simpler way to tackle this question. – nejimban Feb 22 '25 at 14:00
  • 1
    the crucial thing is that by general theory and the fact that for $x$ near $0$ we have $1-\cos x << x^2$ one can find $p_n \to \infty$ st if $1-\cos p_n=c_n$ then $c_n << 1/p_n^2$ and since $(1-1/p_n^2)^{p_n}$ approaches $1$ quite fast one can show that we can reach any $a \in (0,1]$ by taking sequences $k_ap_n$ - the method in the corresponding $(\sin n)^n$ answer linked above shows how concretely but the crux is the observation above; for $[-1,0)$ one has to use more advanced results that control the parity of the continued fractions approximations but same idea works – Conrad Feb 22 '25 at 17:42

0 Answers0