A sine expansion for $v_p(x)$?

Question

Motivation : Let $n$ a positive integer , show that $2^{n+3} \mid 3^n +7$ has no solutions? and $3^n$ does not divide $4^n+5$ for $n\geq 2$

To solve the problems above, we need to find a nice upper bound for $v_p(x)$, thus for $x=3^n+7$ and $4^n+5$

So, in order to show that $2^{n+3} \mid 3^n+7$ or $3^n \mid 4^n+5$ , has no solutions, it suffices to prove the following:

$\forall n \in \mathbb{N^*} , v_2(3^n+7)\le n+2$ and $v_3(4^n+5)\le n-1$ for $n\ge2$

One famous bound is the following : If $n$ is a positive integer, then $v_p(n)\le \log_p(n)$

But it's not efficient for achieving our bound $n+2$ and $n-1$ , Here's why :

$2^{v_2(3^n+7)}\le 3^n + 7$, but $n+2 <3^n+7$

So, I wandered if one could find a sine expansion for $v_p(x)$ ?

because dealing with sine, would be sometimes better than a complicated function like $v_p(n)$

Especially, to find cool upper bounds like $v_2(3^n+7)\le n+2$ and $v_3(4^n+5)\le n-1$

My Attempts:

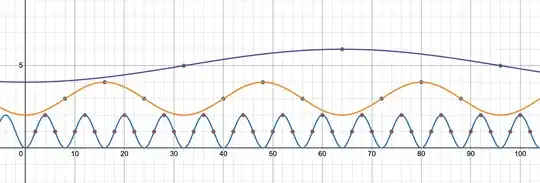
If we consider the following function : $\psi_n(x)=\sin\left(\displaystyle\frac{\pi x}{4^{n}}-\frac{\pi}{2}\right)+2n-1$

Then $v_2(x)=2n$ or $2n-1$ $\Rightarrow \psi_n(x)=v_2(x)$

But $\psi_n(x)$ give us $v_2(x)$ only for some n

Here's the plot of the first $\psi_n$ functions : https://www.desmos.com/calculator/lwtf2ewv9j

with the first even numbers up to $100$ in function of $v_2(x)$ :

How ever, $\psi_n(x)$ is a nice start !

but could someone combine all of $\psi_n$ to get a sine expansion for $v_2(x)$ or of $v_p(x)$ ?

Answer 1

As @Jyrki Lahtonen mentionned before at Can all functions be theoretically iterated succesfully?

A smooth function using trig functions would be:

$v_2(x)=-\displaystyle\frac{\ln(1-\displaystyle\sum_{k=1}^{\infty}2^{-k}\cdot f_k(x))}{\ln(2)}$, with $f_k(x)=\displaystyle\frac{1}{2^{k}}\sum_{j=0}^{2^{k}-1}\cos\left(\frac{j\pi x}{2^{k-1}}\right)$

And similiarly, you could derive a formula for $v_p(x)$,

Here's a plot of this function proposed by @Jyrki Lahtonen:

https://www.desmos.com/calculator/kdtc5mbpox

Answer 2

Proof :

Assume that $x\not\equiv 0 \pmod {2\pi}$ :

Then, $\displaystyle \sum_{k=0}^{n} e^{ikx}=\displaystyle\frac{e^{ix(n+1)}-1}{e^{ix}-1}$

As $e^{ix}-1=e^{\frac{ix}{2}}(e^{\frac{ix}{2}}-e^{\frac{-ix}{2}})$ and $\sin(x)=\displaystyle\frac{e^{i\theta}-e^{-i\theta}}{2i}$

$\Rightarrow e^{ix}-1 = 2ie^{\frac{ix}{2}}\sin(\frac{x}{2}) \text{ , } e^{ix(n+1)}-1 = 2ie^{\frac{ix(n+1)}{2}}\sin(\frac{x(n+1)}{2}) $

$\Rightarrow \displaystyle\frac{e^{ix(n+1)}-1}{e^{ix}-1} = \displaystyle\frac{2ie^{\frac{ix(n+1)}{2}}\sin(\frac{x(n+1)}{2})}{2ie^{\frac{ix}{2}}\sin(\frac{x}{2})} = \displaystyle\frac{e^{\frac{ix(n+1)-ix}{2}}\sin(\frac{x(n+1)}{2})}{\sin(\frac{x}{2})}= \displaystyle\frac{e^{\frac{inx}{2}}\sin(\frac{x(n+1)}{2})}{\sin(\frac{x}{2})} $

As $\Re(e^{ikx})=\cos(kx) \text{ , } \Re(\displaystyle\frac{e^{\frac{inx}{2}}\sin(\frac{x(n+1)}{2})}{\sin(\frac{x}{2})})=\cos(\frac{nx}{2})\frac{\sin(\frac{x(n+1)}{2})}{\sin(\frac{x}{2})}$

$\Rightarrow \displaystyle\sum_{k=0}^{n}\cos(kx)=\cos(\frac{nx}{2})\frac{\sin(\frac{x(n+1)}{2})}{\sin(\frac{x}{2})} $, when $x\not\equiv 0 \pmod {2\pi}$

If $x\equiv 0 \pmod {2\pi}$, $\displaystyle\sum_{k=0}^{n}\cos(kx)=n+1$

Doing this substitution $x \rightarrow \displaystyle\frac{\pi x}{2^{k-1}}$, we get the following :

$\displaystyle\sum_{j=0}^{2^k-1}\cos(\frac{j\pi x}{2^{k-1}})=\begin{cases} \cos\left(\pi x\cdot\frac{2^{k}-1}{2^{k}}\right)\cdot\frac{\sin\left(\pi x\right)}{\sin\left(\frac{\pi x}{2^{k}}\right)}=0 \text{ , if } \displaystyle\frac{\pi x}{2^{k-1}} \not\equiv 0 \pmod{2\pi} \\ \\ 2^k \text{ , if } \displaystyle\frac{\pi x}{2^{k-1}} \equiv 0 \pmod{2\pi} \end{cases}$

The condition $\displaystyle\frac{\pi x}{2^{k-1}} \equiv 0 \pmod{2\pi} \Leftrightarrow \displaystyle\frac{x}{2^{k-1}} \equiv 0 \pmod 2 \Leftrightarrow 2^k \mid x $

Thus :

$\displaystyle\sum_{j=0}^{2^k-1}\cos(\frac{j\pi x}{2^{k-1}})=\begin{cases} 0 \text{ , if } 2^k \not\mid x \\\\ 2^k \text{ , if } 2^k \mid x \end{cases}$

So :

$\displaystyle\sum_{k=1}^{\infty}\frac{1}{4^k}\displaystyle\sum_{j=0}^{2^k-1}\cos(\frac{j\pi x}{2^{k-1}})=\displaystyle\sum_{k=1}^{v_2(x)}\frac{1}{4^k}2^k=\displaystyle\sum_{k=1}^{v_2(x)}\frac{1}{2^k} = \frac{1}{2}\cdot\frac{1-\left(\frac{1}{2}\right)^{v_{2}\left(x\right)}}{1-\frac{1}{2}}=1-2^{-v_{2}\left(x\right)}$

Rearranging we get:

$v_2(x)=-\displaystyle\frac{\ln(1-\displaystyle\sum_{k=1}^{\infty}2^{-k}\cdot f_k(x))}{\ln(2)}$, with $f_k(x)=\displaystyle\frac{1}{2^{k}}\sum_{j=0}^{2^{k}-1}\cos\left(\frac{j\pi x}{2^{k-1}}\right)$