2

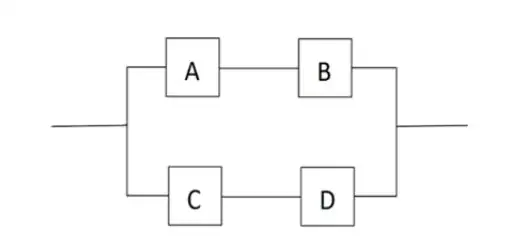
enter image description here

In order for the circuit to work, current must be able to pass from left to right. Each component (A, B, C, D) has an independent probability of failure. Component A has a probability of failure of 0.03. Component B has a probability of failure of 0.04. Component C has a probability of failure of 0.05. Component D has a probability of failure of 0.06.

Given the circuit does not work, what is the probability that components C and D have failed? (Solution says $0.02804$)

I have attempted the question, and found the probability to be 0.7143 however, the solution lists it to be 0.02804, I'm not sure if I have made a mistake, here's how I solved it:

$$P(W_1^c) = P(A \cap B) = P(A)P(B) = 0.0012$$ $$P(W_2^c) = P(C \cap D) = P(C)P(D) = 0.0030$$ $$\text{I understand that I need to find} P(W_2^c | W^c)$$ $$P(W^c) = P(W_1^c \cup W_2^c)$$ $$P(W^c) = P(W_1^c) + P(W_2^c) - P(W_1^c)P(W_2^c)$$ $$P(W^c) \approx 0.0041964$$ $$P(W_2^c | W^c) = \frac{P(W_2^c)}{P(W_1^c) + P(W_2^c)}$$ $$P(W_2^c | W^c) = \frac{0.0030}{0.0042}=\frac{30}{42}\approx0.714285714 \neq 0.02804$$

Y K
  • 35

2 Answers2

2

There are a few issues with your solution.

First, as I read it, you write that the event of failure $W^c$ is decomposed as either the entire top row failing ($W_1^c$) or the entire bottom row failing ($W_2^c$), which is not true. For instance, if the top row fails, but both $C$ and $D$ work, then the circuit is complete.

Instead, think of it like this: the circuit works if either $A^c$ and $B^c$ (corresponding to the top row functioning) or $C^c$ and $D^c$ (corresponding to the bottom row functioning). So, $P(W)=P((A^c\cap B^c)\cup(C^c\cap D^c))$ and hence $P(W^c)=P((A\cup B)\cap(C\cup D))$.

Secondly, your definition of conditional probability is a bit off. In general for events $E_1, E_2$ we have $P(E_1\mid E_2)=\frac{P(E_1\cap E_2)}{P(E_2)}$, so here it should be $P(W_2^c\mid W^c)=\frac{P(W_2^c\cap W^c)}{P(W^c)}$. Notice that $W_2^c\cap W^c=W_2^c\cap(A\cup B)$ (since if the bottom row have already failed, we just need one from the top to fail for the whole system to fail).

Using this, I get the result in your solution list.

muldyr
  • 577
  • 2
  • 8
2

Many conditional probability questions can be solved much nore simply, using the concept of reduced sample space.
This is a typical case of that type.

  • $P(W_2) = (1-0.05)(1-0.06) = 0.813$
  • $P(W_2^c) = 1 - 0.813 = 0.107$
  • $P(C \cap D) = 0.05*0.06 = 0.003$

That's all we need to compute

$P(C\cap D) | W^c) = \dfrac{P(C \cap D)}{P(W_2^c)}$

$$ = \frac{0.003}{0.107} = \frac{3}{107}, \approx 0.02804$$

That is the power of using the reduced sample space concept.
We didn't even bother about branch A-B,
because we know that it must be broken since the system has failed.

If you must, for completeness you can ascribe a value x for $W_1^c$ and multiply both the numerator and denominator by x

true blue anil
  • 48,250