I was playing with Pascal's triangle and noticed an interesting pattern: most numbers (except 1) appear only once (e.g., 2, 3, 4) or twice (e.g., $6 = \binom{4}{2} = \binom{6}{1}$), when excluding duplicates within the same row.
To investigate this further, I wrote a simple Python script to count how many times each number appears in Pascal's triangle:
import math
import matplotlib.pyplot as plt
import numpy as np
a = []
b = []
for n in range(2, 10000):
count = 0
for k in range(n + 1):
for j in range(math.floor(k / 2) + 1):
if math.comb(k, j) > n:
break
if math.comb(k, j) == n:
count += 1
b.append(count)
a.append(n)
plt.plot(np.array(a), np.array(b))
plt.show()
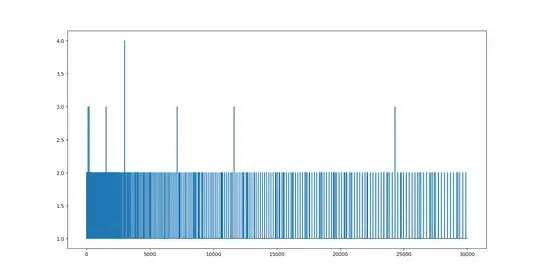
The first number that appears three times is $210$:
$$
210 = \binom{10}{4} = \binom{21}{2} = \binom{210}{1}
$$
The first number to appear four times is (3003):
$$
3003 = \binom{14}{6} = \binom{15}{5} = \binom{78}{2} = \binom{3003}{1}
$$
No number is repeated five times in (1,30000)
I conjecture that for any $ N \in \mathbb{N} $, there exists a number $ n $ that appears exactly $ N $ times in Pascal’s triangle. However, I have been unable to prove or disprove this.
- Is this conjecture true?
- If false, what is the maximum number of times a number can appear in Pascal’s triangle?
Additionally, Assuming this conjecture holds I am curious about the sequence $ a_n $, where $ a_n $ is the first number to appear $ n $ times in Pascal’s triangle. The known values seem to be:
$$
2, 6, 210, 3003, \dots
$$
This sequence does not appear in the OEIS, and finding a closed formula seems difficult due to the chaotic nature of the sequence.
- Can we find an upper bound on $ a_n $? Empirically, $ a_n $ seems to grow rapidly. can we find a function $f$ such that $a_n =O(f(n))$